There is an old saying When the only tool at hand is a hammer, the world appears to be a bunch of nails. Our hammer are the sets {{a,b},{c,d}}, the nails are the points, Axiom 5 defines then how the world appears to us.
Axiom 5 ORI Orientation
Axiom 5.3 is still quite easy to understand: it claims that the relation Q is connected by q-sets. Whatever cut into two pieces, there will be always 2 q-sets that differ only in 1 element to connect the pieces. This claim generalizes Q-Order Axiom 4 ORD as a careful inspection shows: the implications of Axiom 4 establish exactly this type of connection between their left and right sides.
Lemma A 9 shows that any two q-sets can be connected in a finite number of steps.
Lemma A 10 shows how this connectivity extends to Q: any two points are connected through a finite number of q-sets. 
Hence our world is, as intended, connected only by hammers and nails. In a later post about Q-Topology we will see the equivalence to path-connected.
Now the harder parts of Axiom 5, which are intrinsically related to one of the most complicated problems in Algebraic Topology: the problems whether a space has a systematic orientation. In our case there is also a close, independent and direct relation to Group Theory. Both relations will be touched, maybe, in some later posts.
It should be mentioned that there have been related, relevant investigation also in the realm of Petri-Nets, e.g. the Orientation of Concurrency Structures by Olaf Kummer and Mark-Oliver Stehr(1), the Construction of globally Cyclic Orders by Stehr(2) and the proposal of cycloids as basic building blocks by Carl Adam Petri. Again these subjects will be touched, maybe, in a later post.
For our current purpose of motivation only, some picturesque considerations and some simple supporting lemma appear sufficient.
We know already that the points on any circle may be visited one after one in exactly two fashions or orientations: clockwise or counter-clockwise. And –as the following picture shows once more- interchanging (a,b) to (b,a) in {{a,b},{c,d}} reverses the direction.
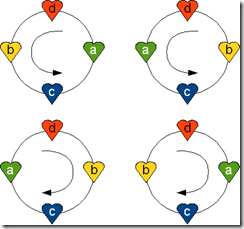
The idea of double-covers in Topology is to split the double-cover later into 2 subsets such that each original element has exactly 1 orientation, applying consistency rules to guarantee a orientation defined as uniform for all elements. From our experience with 5 points, we know it should be sufficient to have a consistency rule just for 5 points and then extend this rule. Let’s see.
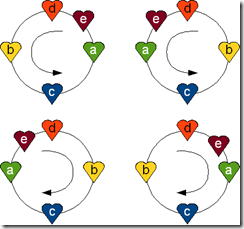
Lemma A 11 
At this stage we know that to be consistently clockwise oriented all quintuples of 5 points must fit into the above definitions and that then the rule expressed as lemma holds.
Axiom 5.2 converts these findings for 5 points into a claim. We claim: there shall exist a split of the double-cover into two single-covers, such that the found rule holds for all quintuples in each of the single-covers. We define then that these Q allow a consistent orientation. Due to Axiom 5.3, there are exactly 2 possible global orientations. Therefore it’s sufficient to define the orientation for any {{a,b}},{{c,d}} to have it defined it for all Q or: there is only one direction of the arrow of time -even though it might be actually cyclic- and its orientation extends from anywhere to everywhere in finitely many steps.
Though somewhat surprising, it’s almost mathematical routine to convert a property found in a specific case into an axiomatic claim: all new model shall have this same property. And it’s relatively risk-less w.r.t.o inconsistencies as the specific case serves as a model in the sense of formal logic consistency.
However and again this is an axiomatic claim, not a fact: the world should be as we think it were, something that can not be proven, only disproven by a found counter-experiment. Similar as in the preceding cases of global claims, we will raise a red flag whenever Axiom 5.2 is actually used. (Question for the interested reader: why there can’t be a counter-experiment to axiom 5.3?)
With these considerations, we end the presentation of the first 5 Axiom-Sets for Q-Orders.
(1) Olaf Kummer and Mark-Oliver StehrPetri's Axioms of Concurrency - A Selection of Recent Results , Proceedings of the 18th International Conference on Application and Theory of Petri Nets, Toulouse, June 23-27, 1997, Lecture Notes in Computer Science 1248, © Springer-Verlag , 1997
(2) Mark-Oliver Stehr Cyclic Orders: A Foundation for Concurrent Synchronization Schemes. University Paris 7, Group Preuves, Programmes et Systemes, December 16, 2003. Part I: Thinking in Cycles





How do these notions relate to standard causal set theory in physics?
ReplyDeleteThank you for this very nice blog.
Simone Severini
http://www.iqc.ca/~sseverin
there is an intentionally -see post about Design Goals- very strong relation.
ReplyDelete(1) As it will be shown in later posts, the Causal Structure of GRT as defined by Hawking is a model for an Q-Order. (Yet the Q-Order concept includes the Causal Structure not only of partially-ordered GRT-Solutions, which are the realm of Hawking)
(2) In another series of post, we will touch the relation to the work done by Sorkin et. al. Yet our approach is fundamentally different. While Sorkin starts with almost any partial order -we skip for the moment Sequential Growth Models- to see whether may by fitted into a a GRT Causal Structure using Poisson-Distributions as a means to coarse grain, we define right from the outset discrete models for Q-Orders as discrete domain and "fit" them just using Q-Topology continuous functions into continuous models of Q-Orders alás (1).
(3) To my own surprise -though I was looking for it- it turned out that the discrete models admissible as Q-orders are exactly the Concurrency-Structures introduced by Petri now 34 years ago. This will be touched by another series of posts.
To me 1+2+3 are quite exiting ..
Yours
Cornelio
(and thanks for the kind comment)
Postscriptum:
ReplyDeleteI have your article
"Quantum Graphity: a model of emergent locality
Authors: Tomasz Konopka, Fotini Markopoulou, Simone Severini, arXiv:0801.0861"
on my deep-reading list ... and had already a first look some time ago.
Yet my background in the math & phys you are using is not -hopefully only not yet- strong enough to dare a post on the relation (as there may be pieces still missing in Q-Orders).
Sorry for the late replay.
ReplyDeleteI have read your very interesting posts concerning with the idea of relativity.
Is there a paper (like a unique pdf) in which I can read the entire description of the theory?
Thanks a lot for your time,
Simone