We had again to modify the definition in two aspects: (1) Taking into account,as we did before when defining the topology that not all elements are places, and (2) introduce some means to connect the locally defined linear structures.
While the Light-cones are the underlying combinatorial structure from General Relativity to model the Causal (or Conformal) Structure, it seems that totally normal neighborhoods serving as charts and the atlas formed by a subset of the class of totally normal neighborhoods are the proper candidates upon which to model the combinatorial equivalent for the Projective Structure.
In my last version for the Q-Space Axioms, I committed a terrible conceptual mistake, which for its detection and clean-up took some time. Mislead by the appearance of the concept of geodesics as if something global yet based on only locally defined properties, I introduced a similar global relation G with local properties. In the second intent, I limited the definition to a pure local G yet this way I lost the connection from local context to local context, which for manifolds is naturally provided by their atlas of charts.
Axiom Set 3 Linear Q-Spaces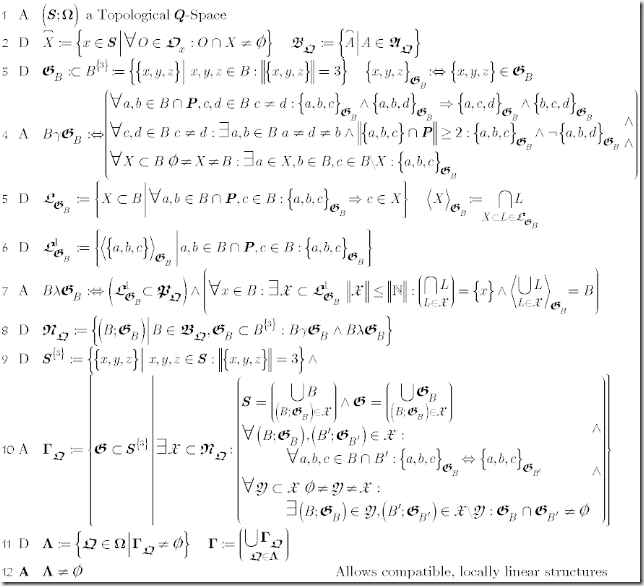
(1) As before, take Topological Q-Spaces as departing point. (2) As before introduces the topological closure and the closed hull of Alexandrov-Sets (=Double Cones) as base-set.
(3) Defines as strictly local relation G within a base-set.
(4) Define 3 properties required to make G a useful Local Linear Structure:
Before continuing, remember that in our topology not necessarily all elements are closed. We singled out one set, the set of Places as not-open, while all others are open.
(4.1) may be called the line property: 2 places define a line i.e. if two different elements c and d are collinear to the same places a and b, then they are on the same line.
(4.2) may be called the separation property: different elements differ in at least one line and any line contains at least two places.
(4.3) may be called the connectivity property: it’s possible to get from anywhere to anywhere in a final number of linear steps.
The combination of (4.1) and (4.2) imply that locally G satisfies the axioms for Incidence geometry: all lines have at least 2 places, two places define exactly one line and finally any 2 different elements are on at least 2 different lines, in our case even stronger: 2 different lines with each at least 3 elements.
(5) defines linear sets i.e. those that with any 2 places contain all locally collinear elements. The <linear set generated by a set of elements> is the smallest linear set that contains them all. The concept of a generated linear set allows later to introduce a combinatorial concept of linear independence.
(6) introduces the set of 1-dimensional linear sets or lines.
The predicate (7) connects lines to the previously topologically defined paths: all lines are paths. This turns lines and hence the local linear structure into a topological invariant. The predicate more over requires that the whole linear structure may be densely generated at each element that is that there is a countable set of lines all containing this element, which generates the whole neighborhood.
(8) defines Normal Blocks as equivalent for totally normal neighborhoods i.e. a block and a local linear structure, right as the definition of a totally normal neighborhood requires a specific affine connection .
(9) introduces the base set for global G, which –as it appears in (10)- is nothing else but the another expression of forming an atlas out of totally normal neighborhoods.
(10) defines the class of global G, formed taking subsets of Normal Blocks. Such a subset has to meet 3 conditions: (10.1) its blocks have to cover the whole set, where the global structure is just the join of the local linear structures. (10.2) The local structures have to be compatible, i.e. agree on shared subsets and finally (10.3) the whole subset of normal blocks has to be connected by means of local linear structures with shared subsets. Actually (10) was modeled following the idea of an atlas of compatible charts for a manifold.
(11) Define the class of Q-orders that allow such a global G and the class of these.
(12) Simply asks that this class is not empty.
Going back to Totally Normal Neighborhoods of Lorentz-Manifolds. All points in a Totally Normal Neighborhood are connected by at most one geodesic, whence different points differ at least in one geodesic. A geodesic relies in its definition on the affine connection. Obviously lines are paths in the underlying topology. In case of standard Lorentz-Manifolds, just 4 lines are sufficient to generate the whole neighborhood. Totally Normal Neighborhoods define charts, which in turn for a fixed affine connection define jointly an atlas, which obviously is connected for connected manifolds.
Voilá exactly what the axiom-set 3 claims for Linear Q-orders.



