Linear Q-Spaces – Second Intent

While the Light-cones are the underlying combinatorial structure from General Relativity to model the Causal (or Conformal) Structure, it seems that Normal Neighborhoods and Normal Coordinate-Systems (alas the Inertial-Frames or the heuristic base for the Einstein Equivalence Principle) are the proper candidates upon which to model the combinatorial equivalent for the Projective Structure.

In my last version for the Q-Space Axioms, I committed a terrible conceptual mistake, which for its detection and clean-up took some time. Mislead by the appearance of the concept of geodesics as if something global yet based on only locally defined properties, I introduced a similar global relation G with local properties.
Now G will be a strictly local relation with only local properties.
Here is the new Axiom Set 3 titled Linear Q-Spaces.

Axiom Set 3 Linear Q-Spaces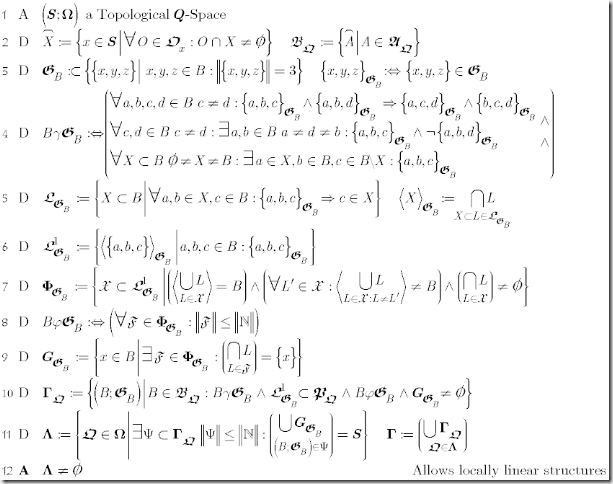

(1) As before, take Topological Q-Spaces as departing point. (2) As before introduces the topological closure and the closed hull of Alexandrov-Sets (=Double Cones) as base-set.
(3) However defines G as a strictly local relations within a base-set.
(4) Define 3 properties required to make G a useful Local Linear Structure:
(4.1) may be called the line property: 2 points define a line i.e. if two different points c and d are collinear to the same points a and b, then they are on the same line.
(4.2) may be called the separation property: different points differ in at least one line.
(4.3) may be called the connectivity property: it’s possible to get from anywhere to anywhere in a final number of linear steps.
The combination of (4.1) and (4.2) imply that locally G satisfies the axioms for Incidence geometry: all lines have at least 2 points, two points define exactly one line and finally any 2 different points are on at least 2 different lines, in our case even stronger: 2 different lines with each at least 3 points.
(5) defines linear sets i.e. those that with any 2 points contain all locally collinear points. The <linear set generated by a set of points> is the smallest linear set that contains them all. The concept of a generated linear set allows to introduce a combinatorial concept of linear independence.
(6) introduces the set of 1-dimensional linear sets or lines.
(7) defines a set of Frames i.e. minimal subsets of mutually linear independent lines (7.2), which generate the whole set (7.1) and are fixed at some point (7.3).
(8) Is a later required technicality: a Frame should be countable at least.
(9) singles out the anchor-points for Frames.
(10) defines for a Q-Order a Locally Linear Structure (though without metric part yet): all those pairs of a base-set B and a relation G defined on B such that it defines a linear structure on B (10.1), every line is at the same time a path in the underlying topology (10.2), all frames are at least countable (10.3) and finally there is at least one anchor point (10.4). Please note that there might be more but only one G i.e. the same base-set may carry more but one linear structure. Finally a Locally Linear Structure is a topological invariant, as a local homeomorphism takes lines to lines (consequence of 10.2).
(11) Selects all those Q-Orders for which there is a corresponding LLS such that there is a countable subset, whose anchor-points cover the whole set. The final LLS is just the union of LLS for all Q-orders.
(12) Just claims that there are Q-Orders with a Locally Linear Structure

Going back to Normal Neighborhoods of Lorentz-Manifolds. These are defined by selecting first one anchor-point (in the Einstein-concept the famous free-falling-observer). All points in a Normal Neighborhood of this anchor-point are connected by at most one geodesic, whence different points differ at least in one geodesic. All points connect by means of a geodesic to the anchor-point, and finally there is at least one frame –the normal coordinate system at the anchor-point- that generates the whole set. Obviously lines are paths in the underlying topology. Finally there is a Normal Neighborhood for any point. The dimension (8) for Frames is just 4. And the second-countability for Lorentz-Manifolds implies the countability restriction in (11)
Voilá exactly what the axiom-set 3 claims for Linear Q-orders.

Next step will be to explore the combinatorial elements of connections when expressed as mappings of frame-sets.