Lines, Cuts and Dedekind

Reformulated without changing its essential content.
Axiom 7 finally ties together classically continuous and classically countable models. As shown in a later post, it defines a new type of Topology valid for both.

Axiom 7 Continuous 

We will walk through the construction step by step.

Step 1: Lines 
Here the second definition introduces sets, where all of its elements are q-related. Then the first line defines as Lines maximal sets of this type. If one accepts the Hausdorff-Maximal Principle for chains of partially ordered sets (or equivalently the Axiom of Choice), then Lines is actually a non-empty set and for any totally q-related set there is at least on containing line.

Step 2: Generalized Dedekind cuts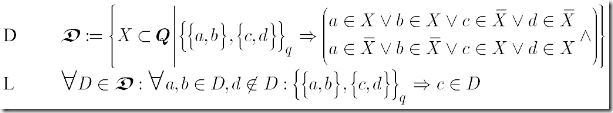
Traditionally a Dedekind cut splits an ordered set into two halves, one below the other. This notion doesn’t make sense on a circle.  Now consider {a,b} as an interval on a line or a circle, then a set is defined as Generalized Dedekind cut, if with endpoints it contains either the interior of the interval or its complement, which on a circle is again an interval; likewise if we would work with the 1-point compactified Real numbers, yet there –without compactification- also the traditional cuts would do.

Step 3: Borders of a Generalized Dedekind cut and what a cut cuts
As border of a Generalized Dedekind cut we define all elements, that are not properly contained in some interval in D, properly means that there should be at least one complementary element outside. A cut cuts a set, if there are elements inside and outside the cut.

Step 4: Line-Limits of a Generalized Dedekind cut
Step 4 is crucial in the whole construction. Actually we are only interested in limiting points on lines, yet for these we will accept only those border-elements as true or objective limits, that do not depend on a specific cut, i.e. when the piece cut-out by two cuts are the same, then there should be –if any- the same limit.

Step 5: The Symmetry-Axiom

In the traditional definition of a Dedekind-cut, either the lower set has a maximal or the upper set has a minimal element, whence crossing the border a maximal element becomes minimal vice versa. 

Step 6: The Cut-Axiom

After these lengthy preparations, the final axioms is short: all Lines should have well defined limits for their pieces, when cut by a Generalized Dedekind cut .

Some Remarks:

1. The basic idea for this type of Generalized Dedekind-cut for partial orders appears already in early papers of Carl Adam Petri. While keeping the basic idea, our definition of a cut itself is different and not only limited to combinatorial i.e. countable partial orders. Yet Petri was the first to note that Dedekind-complete for partial orders might be something quite different than rather requiring classical continuity on all lines (respectively all completely ordered subsets).
2. Nonetheless, for sets consisting only out of a single line or that are totally ordered sets, our definition is equivalent to the one introduced by Dedekind. Hence the Real Numbers are Dedekind-complete respectively –continuous, while the Long Line and the Long Ray are not. And –as intended- the Real Circle is Dedekind–continuous.
3. In earlier attempts –see older parts of this BLOG- I tried to avoid the use of the Hausdorff principle respectively the Axiom of Choice, due to their non-constructive character. These attempts failed so far. So to escape from being stuck in an non-essential detail, I finally accepted the Definition for Lines as a building block.

This ends the presentation of the 7 Axiom-sets for Q-Spaces.