The trapped Arrow of Time – Part I

Obsolete by the Great Simplification … yet still useful for heuristics

The Axioms 1-5 allow to speak about q-sets –our hammer- and points –our nails-, yet we don’t have a space where to put eventually constructed buildings –physical processes-.

The wrong way to get a space would be simply assume it, as Einstein showed convincingly a century ago refuting thereby Immanuel Kant, who another century before had declared space & time as logical aprioria beyond material experience.

There is a second caveat already raised by Einstein –see The Challenge-: though a specific space & time may be extremely practical for a description and hence a necessary heuristic tool, the Physics described should not depend on the specifics of the used space & time: Any space & time should do, as long it produces the same pattern of coincidence.

However –advancing results to be proven in later posts- some additional notes seem necessary:

• Einstein writes about point-events, where only point is the mathematical essence while event is already an interpretation, which apparently turned into a misleading trap for many, many, when they tried to identify the point-events of Einstein with quantum-leap-events from Quantum-Mechanics as introduced by Niels Bohr and Werner Heisenberg. At least I myself was caught in this trap until very recently, though Wolfgang Pauli –as I found out only after getting out of the trap- already noted in 1953 that this identification is false: due to the uncertainty principle QM-events can never ever correspond to closed GRT-points. This is a basic fact of physical life, by no means subject to, less result of impossibilities of observation, as what not is, can not be observed either, notwithstanding bad results from bad observations. It’s more over a structural property and not a consequence of erratic behavior of nature: we hold with Einstein God does not play dice.
• The principle of General Covariance, even more its expression as diffeomorphism covariance, is for Einstein a sequitur of the idea of background independence, yet he never stated anywhere that the realm of Differential Manifolds would be for him the only domain for admissible Coordinate-Systems. As long as we conserve the pattern of coincidence other Coordinate-Systems may do as well (and should do). We are about to show –even though we still have a long road ahead- that Q-Orders might be another, more general candidate.

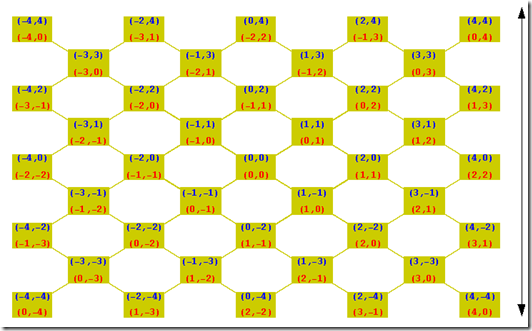
There is another old saying The reinvention of the wheel results easier with a model at hand, so before continuing lets introduce a a model.

The above highly regular structure has two types of “points”, boxes and connectors. To illustrate Coordinate-Systems just as labels, we have labeled the boxes twice, once in blue, once in red, connectors in this simple model apparently need no own labels, as they can be uniquely identified by their limiting boxes. The arrow on the right indicates the possible directions.

Some q-set using red labels {{(0,-4),(0,-2)},{(0,-3) ,(0,-1)}}
The same using blue labels {{(-4,-4),(-2,-2)},{(-3,-3),(-1,-1)}}
A connector in red: {{(0,-4),(0,-1)},{{(0,-3) ,(0,-2)},(0,-5)}}
A connector in blue: {{(-4,-4),(-1,-1)},{{(-3,-3),(-2,-2)},(0,0)}}
Parts of a red line {{(m,2n),(m,2(n+1))},{(m,2n+1) ,(m,2(n+1)+1)}}
Parts of a blue wave {{(m,2n),(m,2(n+1))},{(m+1,2n+1),(m+1,2(n+1)+1)}}
… much more on this in a later post.

The shown grid may be considered as just a window to larger grid, that extends above and below, left and right, yet looking only on the window there is no way to tell whether the grid will extend to eternity respectively infinity or will bend somewhere, somehow returning into itself.

Final observation: take the grid as such, i.e. it’s located nowhere nor occupies anything else. Obviously its representation may need pixel on a screen, bits and bytes in some memory, ink and paper elsewhere, but all these representations, including those that use labels as their means of representation, are only shadows as Plato would have said of the idea grid.

Advancing in content, the picture may be considered as a window on a 2-dimensional discrete Minkowski-Space, once labeled as usual with a time- and a space-coordinate, once with mixed 2 space-time coordinates as first introduced by Kurt Gödel. In the latter form it’s also known as Petri-Grid, as it is a cornerstone in Carl Adam Petri’s General Net-Theory.

Please note that all this is until now pure interpretation of two, among many other, possible label-systems, yet as the labels considered as numbers may reflect in their arithmetic knowledge about the underlying structure, the above chosen labels seem to be useful, each for a different purpose.

Yet the picture has also another interpretation as the structure of an one-dimensional discrete Random Walk, which in turn is the discrete equivalent for the Diffusion-Equation.

Now this equation is the real counterpart to the one-dimensional imaginary Schrödinger-Equation, which models the 1 dimensional harmonic oscillator, whose solution-structure at minimal energy can be represented by Génesis (more about Génesis and Q-Orders).

Génesis is not only the smallest possible Q-Order, but also corresponds to the smallest possible folding of the above defined blue waves.

Hence if our Hauptvermutung is correct and all falls neatly more or less in its place, then the empty discrete 1-dimensional Minkowski-space is not empty at all, but rather constituted not filled by zero-point energy waves, just as it should be … but this nice result is still many, many posts away.

There is a third caveat, this time from Logic. Except Axiom 5, all preceding Axioms stayed within First Order Logic, i.e. referred to individual elements, not to properties of non-constructive sets (Obviously the domains (Q,Q) themselves are many times non-constructive). Though we used already Circle as a heuristic means, talking formally about the Geometry of Space & Time will require to talk formally about sets and their properties, relations among sets and their respective properties and finally functions and sets of functions and their properties.

And here we are in some very fundamental troubles for 2 reasons:

1. The risk of circular nonsense-definitions ala Bertrand Russell or the famous lying Cretans.
2. The almost theological decision to accept or not to accept the Axiom of Choice (or variants, like Zorn’s Lemma and others)

Well, with respect to the first we will stick to some typographic and definition-discipline to avoid –hopefully- trivial definition pitfalls, using different typos for different levels of classes:

1. Small letters for elements, CAPITAL letters for sets, two small letters (or more) for relations among elements.
   Bold letters refer to sets defined before, as we use one of the standard conventions to name Natural Numbers, Integer, Real, Complex and finally Quaternion (or Hamilton Numbers).
   Sometimes we use a subscript to indicate that the definition is to be understood as local i.e. as attached to some specified element(s).
2. Fraktur letters for Sets of Sets and their elements, hence in their definition (:=, :<=>) on the right side appear either sets of level 1 as elements or the elements are taken out of an already defined set of this level.
3. Greek Letters for Sets of Functions/Relations and their elements
4. Though we use recursive and implicit definition as a powerful tool, only primitive recursion is used (with a single, harmless exception sometimes: the implicit definition of equivalence classes).

There will be –maybe- a later post explaining in more detail the whole symbolic language, notation and logical mechanics used. Yet I fear that a 5 pages “must read first” primer about language and notation had been counterproductive. Therefore I hope that the actual snippets together with their verbal transliteration and picturesque illustration are sufficient to capture the intended meanings.

With respect to the second, we accept the Axiom of Choice, yet will try to avoid its usage whenever possible with reasonable effort or else raise the red flag.

This ends the long introduction for Axiom 6.