Obsolete by the Great Simplification … yet still useful for heuristics
After the long introduction of Part I with so many caveats based on painful experiences, here the
Axiom 6 Topology 
As final goal we will construct Q-Path-Topologies, that is the category of topological spaces that correspond precisely to Q-Orders. The construction is done in two steps: first in this part we introduce a first topology for Q-orders, still too general in that it still does not encode completely the orientation by solely means of topology. This will be done in the next step by means of the Q-Path-Topology.
While the definition of Q-Path-Topology adds additional axiomatic constraints on q-orders, once done, we may just start with a Q-Path-Topologies, add a global constraint, that exclude weird paths, and obtain back our underlying Q-order.
As expressed earlier, the Hawking(1)-Topology for GRT shall be one model for Q-Path-Topology and the known Petri-Topology for some discrete Concurrency Structures another. Yet there is a large list of other models, like the Complex Plane, the Quaternion, alas the Minkowski-Space, all one way or the other related to our Leitmotif General Relativity Theory and Quantum Mechanics.
We start out with most simple set, which initiated our reasoning, Lines. Axiom 6.1 defines Lines as a level-2 set, where each two distinct elements of each of its level-1 member-sets –a single piece of a Line- satisfy two conditions:
- They should be members of some q-set i.e. share some circle.
- If there is a q-set that separates them, than at least one other element of this q-set should be also member of this Line.
We note that all one element-sets are trivially Lines and advise –why will be seen later- that this definition requires the Axiom of Choice.
To grasp the origin of the second condition, we have to take a step backward looking first at Q-convex sets.
We note that the empty set and the whole universe are Q-convex sets. Due to the symmetric definition, the complement of a Q-convex set is Q-convex; a surprise may be for some: though obvious for Circle, not-so-obvious for a Line; yet –as one example with more detail in a later post- the Real Line and the Real Circle considered as Q-orders are equivalent, as they are in usual Topology after relatively harmless yet very useful 1-point compactification … and both have hence isomorphic Q-convex sets.
Lemma A 12 then states that with every separated pair {{a,b},{c,d}} a Q-convex set contains at least one of the sets in-between as defined in Q-Order Axiom Lemma 7 and sketched in the corresponding picture.
Finally, Q-convex does not require that any pair of 2 points inside are connected by an in-between set, only those that share some circle, not much of a surprise as our Lines have –among other- time-like curves of General Relativity as conceptual input: not any two points in GRT are time-like connected either; if, then in-between-sets between closed points correspond to the basis of the Alexandrov-II Topology as named by Stephen Hawking in the already mentioned article(1) and detailed –maybe- in some later post. (There is also another, the Alexandrov-I Topology, both named after the same Russian Mathematician Aleksandr Danilovich Aleksandrov, yet with completely different properties. We will need both, hence I and II).
Please note that Lemma 11 still does not need the Axiom of Choice, as the Lemma itself gives sufficient constructive means. The problem arises, when the second condition of the definition in Axiom 6.1 asks us to pick out single elements, where the choice of one element may exclude some others: as imaginable by looking on the pictures or based on the above reasoning, not all pairs of elements in the in-between set necessarily share some circle .. yet this is required by the first condition. It’s here where all the choice-trouble starts. Let’s cross fingers and believe that Lines do exist.
constructs for each point a level-2 set of Lines, those on which the point is encircled by at least 2 other points, as we seen in the previous example. In traditional language one might call them the Line-Intervals that contain the point in question.
I’m afraid, at this point the non-mathematicians will definitively stop reading this BLOG, unless we explain picturesque what we’ve done, advising before that the choice-trouble itself can not be visualized; nobody can see infinite many distinct points as distinct and infinitely close to each other -only imagine maybe- but here is the cause of the problem. Those mathematicians, who find picturesque explanations inappropriate –either you know or you don’t- may skip the pictures.
In the above grid, we will have a look on some of the intervals of the set of Intervals L(0,0) belonging to (0,0).
A blue interval for (0,0) : {(-1,1), {(-1,1),(0,0)}, (0,0), {(0,0),(1,-1)}, (1,-1)}
a red one {(0,1), {(0,1),(0,0)} ,(0,0), {(0,0),(0,-1)}, (0,-1)}
(Recall: connectors have no labels, they are identified by their adjacent points i.e. {(1,1),(0,0)} or {(0,-1),(0,-1)}
As indicated by the arrows, we have selected one out of the two possible directions, downwards. Obvious, the definition of an interval does not depend on the coordinate-system -blue or red- is a matter of convenience, nor on the direction chosen.
An interval includes all points between its endpoints on the same Line. Yet different to the usual, it’s not sufficient to give only the endpoints of an interval, as the following blue examples shows:
{ (0,2), {(0,2),(1,-1)}, (-1,1), {(-1,1),(0,0)}, (0,0), {(0,0),(1,-1)}, (1,-1) }
{ (0,2), {(0,2),(1,1)}, (1,1), {(1,1),(0,0)}, (0,0), {(0,0),(1,-1)}, (1,-1) }
Both intervals have the same endpoints – (0,2), ( 1,-1) - yet mean different paths.
Be aware of the above note about the Q-order equivalence of Real Line and Real Circle. For Q-orders not only the traditional Intervals but also their set-complements (!) on a line are Q-Intervals. This turns out to be no drawback, on the contrary will facilitate the construction of measures on Q-Spaces, as to be shown in a later post.
The Line-Intervals belonging to one point, hence form by set-inclusion a natural upper-complete partial order or upper-set allowing the construction of something similar to a set-filter belonging to that point, expressed more formally:
Lemma A 13
We might have continued directly, coming up most probably with results similar to Keye Martin (2,3), yet decide a small detour, among other as their models do not include discrete model, essential within our framework. To understand, let’s have a look on the usual definition of what is a Topology and some of it’s most essential properties.
Lemma A 14 Topology 
The above states first the normal Axioms for a Topological Space plus two crucial properties: that all elements shall be distinguishable by means of their neighborhoods and that the space as such shall be connected, i.e. going by neighborhood in neighborhood in finitely many steps I can go from anywhere to everywhere. Then we recall the definition for Closed sets and that a Closed Set contains all its points of contact, which leads to the definition of open and closed points. In our context important properties are that in a distinguishing, connected topological space, no point can be both, open and closed, and that in a countable space of this kind not all points can be closed.
Axiom 6.3
retakes the results from Lemma A.13, and defines as l-closed those elements that can be separated from all others by a line or likewise, that are equal to their l-contact set.
Before continuing, let’s have a look on our Grid-Model, what might be open and what might be closed points. As one easily verifies, all connectors are closed, while the boxes are not, as their connectors x can not be separated by a line in Lx.
Now we continue with
Axiom 6.4-5 
We define the subset of open Line-intervals of a points, and a Level-3 set built with sets of open Line-intervals, where the sets of this Level-3-set Lx (Big Lambda in the formula) contains for every open Line-interval just one representative.
In our model, we use different color-families –the green and the margenta family- to illustrate chains of intervals (one contained in another with more tones). 
Lemma A 15 
Please keep in mind that boxes are open by definition, there fore the blue set {(4,2),{(4,2),(3,1)},(3,1)} defines an open Line-Interval for the connector {(4,2),(3,1)} as the set {{(4,2),{(4,2),(3,1)},(3,1)}} is a member of L{(4,2),(3,1)}.
Axiom 6.5 finally uses Lx to construct the actual Filter Ux (a level-2 set). The sets U in Ux simply correspond to the union of the point-sets of sets of Line-Intervals or said differently but equivalent uX projects L-sets into Q. Please note, Line-Intervals and Ux are strictly locally defined, i.e. attached to some point.
We note that Ux inherits Lx from the filter properties.
Lemma A 16 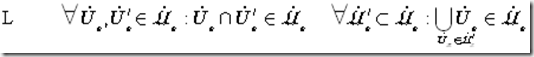
Axiom 6.6 introduces the Topology.
The Open sets of this Topology O are those sets that for each l-closed point contain some set of its corresponding open filter-sets Ux. We leave the verification that Axiom 6.6 defines a topology as previously described in Lemma A 14 to the interested reader, yet using Lemma A 16 it’s not so difficult either.
However there are counter-examples in already in the case of countable base-set Q, showing that neither distinguishing nor connected follow from previous Q-Axioms and this definition of O-Topology.
Axiom 6.7-9 
We claim connectivity in a stronger form: all Lines shall be topologically connected, a necessary condition if we would like to have Lines as continuous images of paths (as continuous mappings of [0,1]), essential for the Hawking-Topology. The connectivity in Q was already established in Axiom 5.
Similar we claim that the open filter-sets Ux form a base for the neighborhood-filter Ox and hence for the whole topology O.
Axiom 6.9 encodes a center piece of GRT: the cone formed by open time-like curves through a point is open (4). Whence automatically satisfied in countable and finite cases, it was much harder to find as essential axiom for the other Q-structures. We will introduce a model to discuss this in the next post.
Finally, just for the sake of consistency in our definitions:
Lemma A 18 
that is l-closed w.r.t. lines and close w.r.t. the topology have the same meaning.
This ends the presentation of Axiom 6.
1 S. W. Hawking A.R. King and P. J. McCarthy, A new topology for curved space-time which incorporates the causal, differential and conformal structures Journal of Mathematical Physics Vol. 17, No 2, February 1976
2 K. Martin and P. Panangaden. Spacetime topology from causality arXiv:gr-qc/0407093v1
3 K. Martin and P. Panangaden. A domain of spacetime intervals in general relativity arXiv:gr-qc/0407094v1
4 Stephen Hawking, Roger Penrose, The Nature of Space and Time, Princeton University Press, 1995, ISBN 0-691-05084-8


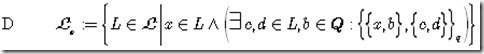





No comments:
Post a Comment