Going in Circles - Part I

Strange as is may sound, to me Axioms are not just formal statements –obviously if we like to do Mathematics later on, they have to be also formal statements in some formal language-, but rather the intent to express as precisely as possible a concept found in reality, Plato would have said an idea.

In this post we’re going to show for 3 of the first 5 Axioms how they have been found and what was the essential input for the remaining 2 of them. Our basic idea are the circle and relations among 4 distinct points on that circle, expressed by an unordered pair of 2 unordered pairs.

Axiom I Q-Relation

Why this relation? Let’s have a look on a circle and just any 4 distinct points and their possible configurations.

To avoid any premature symbolic interpretation, we use 4 small hearts in 4 different colors to mark the 4 distinct points. Then the simplest way to express the only invariant of these configurations is by stating that the set {red heart, yellow heart} separates the set {blue heart, green heart}, a statement that remains true from which ever side we look on the circle; from before, from behind, from top, from bottom, from left, from right … and anywhere in-between.

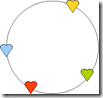
The remaining definitions just introduce short notations for the relation itself and to denote that 4 points occur actually jointly on one Circle.

As easily seen, any 4 distinct points may be grouped into exactly into 1 set of 2 sets. As candidate for an axiom we note therefore (it will be a consequence of our final Q-Order Axiom 4):
Lemma A.1

Any additional statement would need additional information from either some external frame of reference –like the blue heart is on the left- or an additional convention to describe a way how one heart after another may be visited, i.e. an inner orientation. We note that apparently there are just 2 inner orientations.

Axiom 2 Q-Reduced

Axiom 2 RED states then that all shall be expressed in terms of points and circles, such that 2 points which appear anywhere –at any circle- in identical configurations shall be considered identical. And for the sake of completeness, we eliminate completed isolated points.

What happens if a 5th heart enters the game? Let’s see:

The 4 purple hearts with 5 show just the 4 possible positions of the 5th point.

Fortunately we may describe its position exactly using only the already defined relation Q, as the next axiom candidate shows.

Lemma A.2

In words: If 5 points are on a circle and for 4 of them their configuration is known, then the 5th falls in exactly 1 of 4 alternatives (uses the lemma 1).

As a consequence, the configuration of any set of distinct points on a circle may be defined using only the relation Q.

In the finite case, there are (n-1)! circle-configurations for n elements. As stated already elsewhere, the Sumerian used 5, 6 and 7 elements and their configurations as the base for their mathematics and geometry.

Looking on the above configurations, we find a triplet of relations of 5 points that never occurs:

Lemma A.3

It just expresses that {a,b} splits the circle in 2 halves.

What if we have two circles and not only one? Axiom 4.1 and 4.2 deal with these cases.

Axiom 4 Q-Order

Let’s picture the first case.

Obviously there should be some new circles formed by elements of both and the new circles will share the elements a and b. Yet not all combinations of 4 new circles would be mutually compatible (lemma 3). Axiom 4.1 offers the only two choices possible: (an inner {{a,b},{d,e}} and an outer circle {{a,b},{c,f}}) or (a left {{a,b},{c,e}} and a right circle {{a,b},{d,f}}).

Now the second case:

Again not all possible combinations would be compatible. Axiom 4.2 offers the only two choices possible: Either an inner circle with 5 elements {a,b,d,e,f} or an outer circle with again 5 elements {a,b,c,e,f}.

Please note that the terms like inner, outer, left and right have no intrinsic meaning yet. They just may help in seeing the circles.

Finally the third possible case:

Here the original circles are {{a,c},{d,b}} and {{a,f}},{{e,b}} and almost any additional circle is possible, as that there is none at all. Hence Axiom 4 makes no claims for this situation.

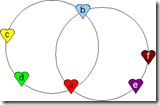
Lemma 1 and 2 were initial working hypotheses (candidates for axioms). We leave it to the reader that now - as intended -they are consequences of Axioms 1, 2, 4.1 and 4.2.

We will go back for a moment to a single circle and show how implicitly there is an order defined as soon as one decides, which points should be beginning and end.

With Lemma 2 already holds the following:

Lemma A.4

This may be used, once fixed a and b to define a partial order.

Lemma A.5

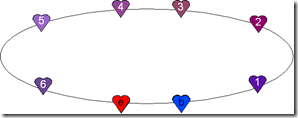
Have a look on the following picture

and you easily verify that {{b,n},{m,e}} as defined for the circle, will order the whole set {1,2,3,4,5,6} as one would expect. Note that inverting the order of (b,e) to (e,b) inverts the order of the set, again as one should expected.

The dual orientation of circles is the underlying principle. The remaining parts of the first 5 Axioms –3, 4.3 and 5- will insure that there is a consistent orientation –up to duality- for the whole Q and in all of it’s admitted circles, by virtue of which in any Interval we may operate as usual with partial orders.