Going Backward, Going Forward – Part I

In the following 3 posts we will go backward and forward through the seven axiom-sets, on one side to get a better feeling for Q-Orders, on the other to relate Q-orders with classically known concepts. The final post will show that the Hawking-Topology is a Q-Order.

Let’s start in this post with some considerations about the Axioms 1 to 5 and their relation to partial orders.
Axiom 1   Q-Relation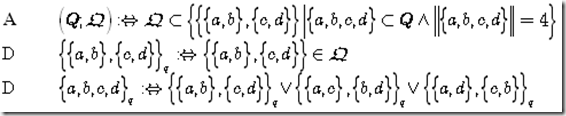

 Lemma F.1   Q-Relation 
  
states that with the proper definitions, any partial order satisfies Axiom I.

Axiom 2 has similar effects for partial orders has it has for Q-Orders:
Axiom 2   Q-reduced

Lemma F.2   Q-Reduced
i.e. we don’t permit isolated points and points that could not be told apart by using the partial order are considered the same. Further on we will consider only reduced partial orders. Please note this condition is weaker than the standard distinguishing conditions.

Axiom 3.1 imposes an additional condition on partial orders, every sequence of three points a<b<c can be completed to have 4, yet Axiom 3.2 follows already from being a partial order.
Axiom 3   Q-regular

Lemma F.3   Q-Regular
  
Please observe that using brute force to prove F.3.2 requires to analyze (3*8)^4=331,776 combinations of binary conditions, which due to internal dependencies may be reduced to less then 6144, but still a substantial quantity, which again for a proof may be further reduced by applying internal symmetries. Instead of wasting three pages with either resulting valid combinations or detailed analysis of symmetries, we just put a small picture and invite the reader to do the latter her- or himself.
 
Suggestions for a 5 lines-proof are obviously welcomed. We let the brute force method being applied by a computer. With respect to F.3.1, we assume henceforth that all partial orders a regular.

Intentionally –it was designed that way- Axiom 4 turns out to be a property of reduced, regular partial orders.
Axiom 4   Q-Order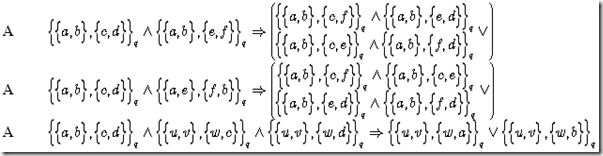

Lemma F.4  Q-Order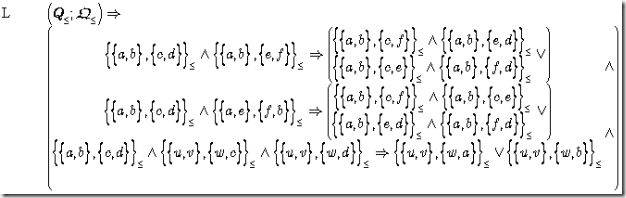
  
Again we will not reproduce the pages of a formal prove, but invite once more to have a look on some pictures.

We break the analysis  of Axiom 5 into two pieces, first the construction of the orientation-set, then the connectivity conditions.
Axiom 5   Q-Orientation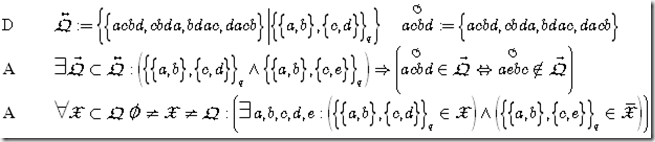

Lemma F 5.1  Q-Orientation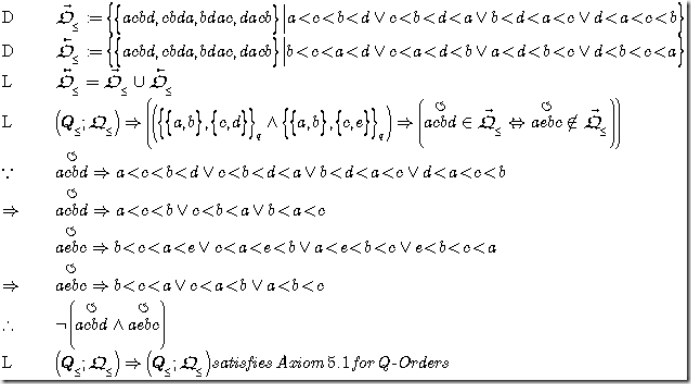

Actually we construct the two orientation-sets, then the F 5.1.3 is direct consequence of the construction, while F 5.1.4 is proven in few steps. This establishes the expected result F 5.1.5: partial orders have an orientation. But please note: the orientation is not the order of partial order itself, as orientation means always oriented cycles.

The final lemma of this post transcribes the connectivity-condition for Q-orders into the language of partial orders.
Lemma F 5.2   Q-Connected

As preliminary result of our comparison Q-Orders versus Partial Orders, we obtain that under relatively weak constraints –Lemmas F.2 and F.3- plus the connectivity-condition –Lemma F.5.2- Partial Orders are models for the Axioms 1-5 for Q-Orders. This will ease the task to establish Hawking-Spaces –alas Causal Sets- as Models for Q-orders, because we can simply rely on the underlying partial-order and are almost done. By default these partial orders satisfy our weak constraints, while –advancing results- the connectivity-condition is one of their key-features.

Yet second this condition points already on a set of minimal constraints that a partial order must comply to become a candidate to be related by whatever structural-knowledge-preserving mechanism to the structure underlying GRT. It turns out that these have to take the form of Second-Order-Predicates, i.e. they can not be expressed as simple statements about relations among points.

Third it appears as if Q-Orders provide a proving-mechanics almost as strong as the transitivity respectively monotony from partial orders, essential not only for proofs but already for constructions like induction or convergence etc., yet without the disadvantage to have to believe that there is a universal beginning and a universal end for all and everything, a non-scientific hypothesis as it can’t be proven nor disproven. (See also Fotini Markopoulou (1)).

As a technical advantage, it will allow us to talk about systems with cyclic behavior –at least during some time-, not only –see Oscillator- a fundamental model in Physics but essential to introduce measurements or without cyclic clocks there is no time and without time there is no measurement at all, as there are no means to measure space as such.

This ends our first considerations about Q-Orders and Partial Orders.

1 Fotini Markopoulou, An insider's guide to quantum causal histories (1999), http://arxiv.org/abs/hep-th/9912137