Name it - Tame it

After almost 3 years of silence -while I was like the mouse in the cage, wheeling around without getting anywhere, here is something new announcing that finally I found something that looks like the combinatorial equivalent of a Pseudo-Riemann Differential Manifolds.
It appears as if all boiled down to find the most appropriate universe of discourse to name the abstract objects I was struggling with. 
Here is the story:

Name it – tame it

When creating new Mathematics -new structures, properties, relations and operations- sooner or later you face a non-mathematical but non-trivial problem: how to name them.

If you use already established names, obviously you have to show that your objects belong to the same category of objects already baptized or at least to the same family that is sharing some typical characteristics while dropping or generalizing others, else an already familiarized reader would be misled intuitively into wrong assumptions and worse false conclusions. 

The most radical approach would be to invent the names themselves that is even new words as sequences of letters that never have been used before. Yet words in common language do not come isolated but as a vocabulary belonging to some common problem domain, a for that problem domain.

Much of Mathematics itself consists in taking some of these words as terms defining their initial meaning that is converting intuition by means of axioms into Mathematics, and then proceeds to derive properties, relations and operations using the tools of mathematical logic while preserving o précising the intuitive meaning of the corresponding term in the original vocabulary.

Geometry itself is a mathematical subject, which started in the Euclidian Geometry using some terms of the Anschaung as still informally defined axioms yet a rigorous argumentation-scheme to derive properties, relations and operations.

It’s formalization starting the early XIX century did not only provide us with new types of geometries, not covered by Euclid himself, but finally with an extremely powerful mathematical tool, Differential Manifolds, which is right at the heart of General Relativity as we know it now.  

However in this context Sheaf-theory shows another way Mathematics adopts common language terminology not as only isolated words but as a vocabulary of meaning-connected words.  Here the imported vocabulary itself is not the object of study but serves or at least aims to serve as an intuitive guidance to comprehend the otherwise completely abstract, purely mathematical structures. I do suspect it was even more and earlier: the imported language served as mind-guidance to its creators while creating the new theory itself.

At its beginning, the mathematical language for General Relativity that Einstein used was Tensor-Calculus, which in turn was developed during the XIX century starting with Gauss. Its real problem-domain was literally Geometry not as an abstract mathematical subject but as a technology used to create the first large-scale exact maps. As the areas were by far greater than Attica, pure Euclidian Geometry and its algebraization by Descartes were insufficient as they did not take into account the curvature of earth. Hence much of the new names for the new mathematical objects were an import from the language of the land-surveyors.

The now most frequently used mathematical language for advanced GRT is the Calculus of Differential Forms as developed by Cartan at the beginning of the XX century. While maintaining Differential Manifolds as a fundamental concept, the Cartan Formalism provides a concise yet very compact hence very elegant language to express complicated relations, yet its full theoretical background includes many concepts from many areas, from Topology to Lie-Groups. That’s sufficient stuff to fill a complete curriculum for postgraduate studies in Mathematics. Therefore most introductory courses into GRT still rely on the original Tensor-Calculus. Yet on the other hand almost all attempts aimed at Quantum-Gravitation start with the Einstein-Cartan form of GRT.

GRT as such combines two rather different concepts: Causality and its rules as defined by Special Relativity and Gravity as modification of the space-time geometry, both connected by Einstein’s field equitation, where -as John Archibald Wheeler put it- "Space-time tells matter how to move; matter tells space-time how to curve."

A closer look on Causality first by Stephen Hawking then by David B. Malament moreover revealed that it comes with its own geometry, named causal structure, whose topology is somewhat related yet not equivalent neither to the topology created by gravity nor the topology of the underlying Differential Manifold. Similar, the effects of Gravity can be completely described by the geodetics of free falling particles, which are both causal paths w.r.t. Causality and extremal paths w.r.t. Gravity. Seen as Geometries, the first correspond to conformal Geometry, the latter to projective Geometry, which together completely define a Pseudo-Riemann Differential Manifold.

The concepts and tools provided by the above 2 structures are not sufficient to express neither of Einstein’s famous equations i.e. neither E = M c² of SRT nor the Field equation of GRT. Worse yet they do not allow to express the special equivalence principle i.e. inertial mass = gravitating mass, leaving it buried inside the formalism of Tensor-Calculus; the more general idea that Physics is the same – anywhere, anytime degenerates into covariance, which was meant by Einstein as an expression for the former not it’s founding.

While it’s rather straightforward to find combinatorial structures to model Causality and the effects of Gravity, actually the causal-structural itself is a combinatorial structure, it turned out to be quite difficult to find an combinatorial substitute for the Differential Manifold itself and its construction and almost impossible in the vocabulary of surveyor’s geometry where the constituents are just maps, alas descriptions. It’s already almost impossible to grasp using this vocabulary the conceptual difference between active and passive Diffeomorphisms as introduced by Carlos Rovelli. Yet without that substitute there is no way neither to find a combinatorial substitute for the Cartan Formalism, even if the latter already eliminated algebraic invariance using geometrical symmetry instead. And without that substitute there is, in my humble understanding, no Quantum-Gravity either.

May be due to my laziness –I did not invest the equivalent of a postgrad-curriculum- may be due to my other limitations, I made countable many attempts to find this substitute, always staying within the traditional vocabulary for Differential Manifolds. Finally I decided to drop this vocabulary all together and to switch to another taken from textiles. Now everything fits neatly, at least up to the combinatorial equivalent of a Pseudo-Riemann Differential Manifold, yet still –and fortunately- without metric.

As mathematical structure beneath we use connected locally path-connected Topologies, yet weaker than the usual Haussdorff-Space of Differential Manifolds. Our category of topologies includes discrete models, alas Petri-Nets. What in the Haussdorff case are the paths of Jordan-Curves is generalized into ropes.

In my framework for new terminology, you may think about Einstein’s Universe as a patchwork of many fabric pieces, tied together by compatible seams. The seaming process and its compatibility condition resemble the classical construction of a Differential Manifold. Even more: using proper strands that is subsets of ropes -the paths of continuously differentiable Jordan-Curves- and specific seams -patch-wise isomorphic- the resulting quilt is the combinatorial equivalent of a Differential Manifold.

Classical fabric is made out of 2 quite different components, the warp and the weft, where the warp defines a fixed, pre-tensed setting that the weft may transverse connecting; or catching up Wheeler, warps will resemble effects of Gravity, wefts Causality. A weaving process puts both together, where shedding is formally expressed by strands that belong to both structures, as were the geodetics of free falling particles.  

As a result, using the above mentioned proper strands and specific seams, the woven fabric is the combinatorial equivalent of a Pseudo-Riemann Differential Manifold yet without metric.

Up to here the ideas are completed (to follow soon).

More –this time mathematical- heuristics

Let me try to explain what I’m trying to do. [Especially not trying to re-invent the wheel when there are so many proven, useful models at hand].

I’m aiming at Combinatorial General Relativity, as Einstein mentioned at the end of some of his writings as an unsolved puzzle.

Yet “my way” is not the usual top-down –i.e. trying to find quantization-rules on the very top- but “bottom-up” that is investigating in a more or less systematic fashion the implicit and explicit combinatorial elements and structures on each level. Here “causal structure”, based on the work of Stephen Hawking, David Malament and others, is already an almost closed chapter (Q-Orders).

The current “target”: differential manifolds.

Usually a manifold is defined using local homeomorphism between some local neighbor-hoods in the manifold-topology and some local part of a Euclidean space. For the latter normally one uses its algebraic definition (module over some field), gets from there to the usual Euclidean metric and then obtains the topology.

Now there is a completely equivalent set of Axioms for Euclidean Geometries: the famous Hilbert Axioms. Why would one like to use this set? Well, it’s known that there are finite, discrete models that satisfy the first set of Hilbert-Axioms (incidence Axioms for points, lines and planes), yet do not satisfy the second set (Order-Axioms) nor the third (Congruence-Axioms) and where the forth (Parallel-Axiom) is optional.

Not only this, but as v. Staudte, Moufang, Veblen, v. Neumann and others have shown, already the first set allows the construction of coordinates and hence metric, i.e. coordinates and metric arise using incidence relations and nothing else. [And that’s what I understand Einstein had in mind with his remarks].

Incidence relations as “founding ground” have a second great advantage: topological homeomorphisms carry them over automatically, i.e. suitably defined the manifold inherits these relations automatically, while congruence-relations or algebraic properties do not.

The “missing link”: Hilbert takes “lines” and “planes” as primitives (as does synthetic Geometry). So in my next –failed- intent I was looking where to find “lines” and “planes” in the context of Riemann and Pseudo-Riemann manifolds, and voilá there they were: geodesics and totally normal neighborhoods, yet with a tremendous drawback: their definition already requires concepts of the very, very top like the metric-tensor and the exponential map.

So I did a step backward, asking myself: is it possible to introduce lines using ONLY topological concepts? The model at hand: balls and spheres as defined by the usual Euclidean metric.

Next step: is it possible to define balls and spheres without using metric? Well it is. One might use simply connected neighborhoods and simply connected surfaces and, as recently shown, we get nice spheres in all dimensions.

Problem: “simply connected” as concept requires Hausdorff-spaces and imports via Homotopy the whole “World of Reals”, incompatible with my aim to allow also discrete, finite models not talk about my suspicion that it is a far to restrictive assumption for the real World (there are holes almost everywhere). Therefore I replaced “simply connected” by just “locally path connected”.

Next step: given sets of surfaces of locally path connected neighborhoods, what would be a minimal set of axioms based only on incidence and topology that would convert this set locally into something similar to the Euclidean Balls and –Spheres we started with? There a point lies on a straight line between two points iff there are Spheres for each of them that touch each other exactly in that point. More over the Spheres made using Euclidean Distance form a complete order around each point. There are additional compatibility rules among the spheres of different points on the same straight line. Finally “completeness” respectively “coherence” is to be considered i.e. in Euclidean Geometry there is always a straight line that connects them. This again would provoke “continuous models only” already in three dimensions. So I weakened this requirement to: “it should be possible to go from anywhere to anywhere in straight steps” and “if there are intersecting spheres for two points, then there are touching spheres (and hence a line that connects them)”.

Done this, we get a set of definitions invariant under any topological homeomorphism. That means two things: they carry over “automatically” to the manifold (locally of course), but second they produce a natural gauge. (Not such a surprise: there quite many metrics already for the real line, which produce the same topology. For instance the max-norm reproduces the same topology yet has cubes as balls).

Once I’ve got lines, the remainder is almost straight forward, using well known properties from synthetic geometry for triangles and quadrilaterals as axioms required to be able to “construct” coordinates and metrics. Yet (a) they all use nothing but incidence relations (b) are satisfied by usual Euclidean Geometries and therefore (c) inherited –locally- by any manifold.

Adding the additional structure of lines, adds to the compatibility-conditions for an Atlas of “charts with lines”. While the topological part remains –coincidence of topology on intersections-, I’m not yet finished of what is required in my case. [Again not such a surprise, taking into account that a Differential Manifold imposes additional compatibility conditions and that –exotic spheres from 4 dimensions onward- there might be more but only one Differential Structure].

Compatibility-Conditions and polish-up may still take some weeks or months, among other because I’m not sure whether going from “simply connected” to “locally path connected” is to weak, that is at least something similar to “star-connected” might be required (yet this as concept already uses “straight lines” so … ).

Topology and Geometry: Heuristics

This is yet another attempt to define and deduce the two very basic ingredients of the type of structures we would like to use as common underpinning for General Relativity Theory (normally assumed to be continuous) and General Net Theory (for which the so called Petri-Nets are just one example). This time we will concentrate on Topology and Geometry.
Be aware: this is work in progress!

III Geometry

I.0 Initial Heuristics

0.1 Einstein himself

EUCLIDEAN AND NON-EUCLIDEAN CONTINUUM
The surface of a marble table is spread out in front of me. I can get from any one point on this table to any other point by passing continuously from one point to a "neighboring" one, and repeating this process a (large) number of times, or, in other words, by going from point to point without executing “jumps". I am sure the reader will appreciate with sufficient clearness what I mean here by “neighboring" and by “jumps" (if he is not too pedantic). We express this property of the surface by describing the latter as a continuum.

Let us now imagine that a large number of little rods of equal length have been made, their lengths being small compared with the dimensions of the marble slab. When I say they are of equal length, I mean that one can be laid on any other without the ends overlapping. We next lay four of these little rods on the marble slab so that they constitute a quadrilateral figure (a square), the diagonals of which are equally long. To ensure the  equality of the diagonals, we make use of a little testing-rod. To this square we add similar ones, each of which has one rod in common with the first. We proceed in like manner with each of these squares until finally the whole marble slab is laid out with squares. The arrangement is such, that each side of a square belongs to two squares and each corner to four squares.

It is a veritable wonder that we can carry out this business without getting into the greatest difficulties. We only need to think of the following. If at any moment three squares meet at a corner, then two sides of the fourth square are already laid, and, as a consequence, the arrangement of the remaining two sides of the square is already completely determined. But I am now no longer able to adjust the quadrilateral so that its diagonals may be equal. If they are equal of their own accord,  then this is an especial favor of the marble slab and of the little rods, about which I can only be thankfully surprised. We must needs experience many such surprises if the construction is to be successful.

If everything has really gone smoothly, then I say that the points of the marble slab constitute a Euclidean continuum with respect to the little rod, which has been used as a “distance" (line-interval). By choosing one corner of a square as “origin", I can characterize every other corner of a square with reference to this origin by means of two numbers. I only need state how many rods I must pass over when, starting from the origin, I proceed towards the “right” and then “upwards”, in order to arrive at the corner of the square under consideration. These two numbers are then the “Cartesian coordinates" of this corner with reference to the “Cartesian coordinate system" which is determined by the arrangement of little rods.

By making use of the following modification of this abstract experiment, we recognize that there must also be cases in which the experiment would be unsuccessful. We shall suppose that the rods “expand" by an amount proportional to the increase of temperature. We heat the central part of the marble slab, but not the periphery, in which case two of our little rods can still be brought into coincidence at every position on the table. But our construction of squares must necessarily come into disorder during the heating, because the little rods on the central region of the table expand, whereas those on the outer part do not.

With reference to our little rods –defined as unit lengths- the marble slab is no longer a Euclidean continuum, and we are also no longer in the position of defining Cartesian coordinates directly with their aid, since the above construction can no longer be carried out. But since there are other things which are not in influenced in a similar manner to the little rods (or perhaps not at all) by the temperature of the table, it is possible quite naturally to maintain the point of view that the marble slab is a ”Euclidean continuum". This can be done in a satisfactory manner by making a more subtle stipulation about the measurement or the comparison of lengths.

But if rods of every kind (i.e. of every material) were to behave in the same way as regards the influence of temperature when they are on the variably heated marble slab, and if we had no other means of detecting the effect of temperature than the geometrical behavior of our rods in experiments analogous to the one described above, then our best plan would be to assign the distance one to two points on the slab, provided that the ends of one of our rods could be made to coincide with these
two points; for how else should we define the distance without our proceeding being in the highest measure grossly arbitrary?

The method of Cartesian coordinates must then be discarded, and replaced by another which does not assume the validity of Euclidean geometry for rigid bodies. The reader will notice that the situation depicted here corresponds to the one brought about by the general postulate of relativity.

Taken from:  Relativity: The Special and the General Theory, Pages 77-80, A Popular Exposition, 3rd ed. Author: Albert Einstein, Translator: Robert W. Lawson, retrieved from http://www.gutenberg.org/ebooks/36114)

0.2 Appreciation and Findings

Carefully reading the above, there are no numbers involved except counting and actually the whole configuration stays the same when applying heat somewhere, even if rods may need bending not only expansion and angels are no longer right ones. So at the very bottom Einstein talks about Topology and not Geometry, since the whole Geometric content reduces to certain configuration-sets –bended squares-that stay invariant under homeomorphisms.  Please note, that in Einstein's considerations there is explicit geometric content –the construction itself- and there is implicit geometric content, for instance the surprise that thinks workout so nicely or the assumption that rods represent somehow shortest connections.

The question hence is: can we express the above using only means of topology, that is converting the implicit assumptions into to properties of purely topologically defined configurations i.e. without referring to metrics, including angles? The answer is: Yes, we can. Before doing so within the framework of our Q-Topology, some additional Gedanken-experiments.

Einstein starts off with straight rods and squares constructed using the rods. Now straight is itself a concept deeply founded in Euclidian thinking as the shortest connection between to points. We now know, just thanks to General Relativity, that the straightest connection itself is defined by the curvature of space-time, hence not a very good starting point to define space-time. What about square? Well, actually Einstein does not use the whole square but rather only its border. And border is a topological concept. So let’s try what happens if we start with circles, assuming that we’ve got for each point a set of circles surrounding it.

Here we got some points scatter in a plane. Actually they were produced plotting for some points sets of circles surrounding these points, or more precisely some points of these circles.

 

 

 

 

 

Here we have the same plane, yet for 3 points we added 4 circles for each and a straight line that runs through these 3 points. Did we just invent this line? No! If you look closer, wherever two different circles share just a single point, there goes the straight line. Or to put it differently, a third point is on a straight line between to other, if there is a circle for each of the 2 and these circle share exactly this third point. By tweaking Mathematica a little bit more, these 3 would have been part of the original set of scattered points.

Here the same picture without the clutter. There are more relations to discover: If a point is at the 1 point-intersection of two circles, then this point itself has two circles, which intersect exactly with one circle of one point and the other point. This means the relation for three points to be on one straight line is permutation invariant.

 

 

Here we added just a forth circle. As it appears, if two different points are each on a straight line with two other points, then all four are on the same line.
And: a point is just in the middle of two other points on the same line, if it has exactly 1 circle running through these 2 points, met a each by a circle from the opposite point.

And here we got a set of circles that is definitively off the line.
In the case of classical Euclidian Geometry, all the observed relations are easily proven. i.e. they are Theorems. But that’s not our interest here. The point is, that once established, they remain valid at least locally under continuous, bijective transformations, i.e. –topologically speaking homeomorphisms- as they preserve sets, intersections and borders, the only concepts we’ve used so far.

 

 

 

 

 

 

 

These are just two examples of different projections of the same configuration: tossing and stretching has no effect, even if our circles aren’t circles anymore.

 

However, we may not transform circles individually. Here the ellipsis  is the result of trying to transform individually the last circle and the result spells disaster. The ellipsis has still 1-point intersections with other circles yet somewhere else. Transformations therefore affect at least locally complete neighborhoods and we can not transform things nicely, i.e. if some borders are circles and others not, there is no transformation that would turn all at once into circles. 

 

 

A final, drastic example: this transformation leaves the circle-sets as sets intact – each depicted in a different color-, yet suddenly our straight line isn’t straight anymore; well it depends: If we take Einstein and our above observations seriously –i.e. that a straight line is defined by its intersecting circle-sets, whatever these circles or equivalent descriptions may be, then the line is now as straight as it was before. We are just using a different but equivalent set of coordinates to describe the configuration or –what finally becomes the same- it’s the same configuration, only in a different gravitational field.

Now let’s see what happens if instead of circles or ellipses we use something else, for instances, as Einstein did, squares respectively quadrilaterals. Topologically speaking, that is without metrics, they are equivalent anyway.

Apparently in this example and it’s transformation, everything works fine. Yet the next example shows that we are in deep, deep trouble.

 

The straight line runs thru the lower right corner, the center and the upper left corner, yet the central quadrilateral though it touches upper and lower quadrilaterals, it does so not in a single point but in a whole segment.

Gauss and Einstein would say: don’t worry! Just adapt and refine your grid and at the limit everything will be fine.  The next picture tries to illustrate this idea.

 

The smaller the quadrilaterals get, the smaller gets their intersection, which appears as if closing in on the line. Yet Heisenberg now would say: be aware, you can’t always refine to the limit, while Feynman would add: well any point of the segment of intersection is part of a possible shortest path, they just differ in their probabilities. The point with the highest probability will be the point closest to a straight line.  

The first approach assumes that somehow, at least in a small neighborhood, we would already know what straight line means, and then starting from there construct an appropriate grid. This would be in discordance with our whole approach, where we would like to use a given grid to define what straight line means.

The second approach requires tools ways beyond pure topology, and even then remains somewhat circular, as its requires already a metric to define the respective wave-functions, which in turn yield the probabilities, where we would like to deduce the metric using the grid and not use a metric to deduce the grid as peaks and lows of the probability function.

The critical condition, that could not be met easily nor always, was that two circles meet just in one single point. What if relaxing this condition just a little bit? To get a better idea, let’s have again a look on the offline circle, now an offline quadrilateral.

There are appearing differences: the green quadrilateral cuts segments out of blue and red, as they do with respect to green, likewise black cuts green and blue and they in turn cut black. Yet while the green-red and red-green respectively green-blue and blue-green segments are the same, the black-blue and blue-black respectively black-green and green-black segments differ; and that is a pure topological difference, which allows us the distinguish the configuration of black wrt.  blue and green  from the configuration of green wrt. red and blue.

For further considerations we will hence relax “share just one point” to “share just one segment”. As to end the heuristics part, we’ll have a look without further discussion on touching and intersecting spheres and cubes in 3 dimensions.

Linear Q-Space - Third Intent

We had again to modify the definition in two aspects: (1) Taking into account,as we did before when defining the topology  that not all elements are places, and (2) introduce some means to connect the locally defined linear structures.

While the Light-cones are the underlying combinatorial structure from General Relativity to model the Causal (or Conformal) Structure, it seems that totally normal neighborhoods serving as charts and the atlas formed by a subset of the class of totally normal neighborhoods  are the proper candidates upon which to model the combinatorial equivalent for the Projective Structure.

In my last version for the Q-Space Axioms, I committed a terrible conceptual mistake, which for its detection and clean-up took some time. Mislead by the appearance of the concept of geodesics as if something global yet based on only locally defined properties, I introduced a similar global relation G with local properties. In the second intent, I limited the definition to a pure local G yet this way I lost the connection from local context to local context, which for manifolds is naturally provided by their atlas of charts.

Axiom Set 3 Linear Q-Spaces

(1) As before, take Topological Q-Spaces as departing point. (2) As before introduces the topological closure and the closed hull of Alexandrov-Sets (=Double Cones) as base-set.
(3) Defines as strictly local relation G within a base-set.
(4) Define 3 properties required to make G a useful Local Linear Structure:
Before continuing, remember that in our topology not necessarily all elements are closed. We singled out one set, the set of Places as not-open, while all others are open.
(4.1) may be called the line property: 2 places define a line i.e. if two different elements c and d are collinear to the same places a and b, then they are on the same line.
(4.2) may be called the separation property: different elements differ in at least one line and any line contains at least two places.
(4.3) may be called the connectivity property: it’s possible to get from anywhere to anywhere in a final number of linear steps.
The combination of (4.1) and (4.2) imply that locally G satisfies the axioms for Incidence geometry: all lines have at least 2 places, two places define exactly one line and finally any 2 different elements are on at least 2 different lines, in our case even stronger: 2 different lines with each at least 3 elements.
(5) defines linear sets i.e. those that with any 2 places contain all locally collinear elements. The <linear set generated by a set of elements> is the smallest linear set that contains them all. The concept of a generated linear set allows later to introduce a combinatorial concept of linear independence.
(6) introduces the set of 1-dimensional linear sets or lines.
The predicate (7) connects lines to the previously topologically defined paths: all lines are paths. This turns lines and hence the local linear structure into a topological invariant. The predicate more over requires that the whole linear structure may be densely generated at each element that is that there is a countable set of lines all containing this element, which generates the whole neighborhood.
(8) defines Normal Blocks as equivalent for totally normal neighborhoods i.e. a block and a local linear structure, right as the definition of a totally normal neighborhood requires a specific affine connection .
(9) introduces the base set for global G, which –as it appears in (10)- is nothing else but the another expression of forming an atlas out of totally normal neighborhoods.
(10) defines the class of global G, formed taking subsets of Normal Blocks. Such a subset has to meet 3 conditions: (10.1) its blocks have to cover the whole set, where the global structure is just the join of the local linear structures. (10.2) The local structures have to be compatible, i.e. agree on shared subsets and finally (10.3) the whole subset of normal blocks has to be connected by means of local linear structures with shared subsets. Actually (10) was modeled following the idea of an atlas of compatible charts for a manifold.
(11) Define the class of Q-orders that allow such a global G and the class of these.
(12) Simply asks that this class is not empty.

Going back to Totally Normal Neighborhoods of Lorentz-Manifolds. All points in a Totally Normal Neighborhood are connected by at most one geodesic, whence different points differ at least in one geodesic. A geodesic relies in its definition on the affine connection. Obviously lines are paths in the underlying topology. In case of standard Lorentz-Manifolds, just 4 lines are sufficient to generate the whole neighborhood. Totally Normal Neighborhoods define charts, which in turn for a fixed affine connection define jointly an atlas, which obviously is connected for connected manifolds.

Voilá exactly what the axiom-set 3 claims for Linear Q-orders.

Linear Q-Spaces – Second Intent

While the Light-cones are the underlying combinatorial structure from General Relativity to model the Causal (or Conformal) Structure, it seems that Normal Neighborhoods and Normal Coordinate-Systems (alas the Inertial-Frames or the heuristic base for the Einstein Equivalence Principle) are the proper candidates upon which to model the combinatorial equivalent for the Projective Structure.

In my last version for the Q-Space Axioms, I committed a terrible conceptual mistake, which for its detection and clean-up took some time. Mislead by the appearance of the concept of geodesics as if something global yet based on only locally defined properties, I introduced a similar global relation G with local properties.
Now G will be a strictly local relation with only local properties.
Here is the new Axiom Set 3 titled Linear Q-Spaces.

Axiom Set 3 Linear Q-Spaces

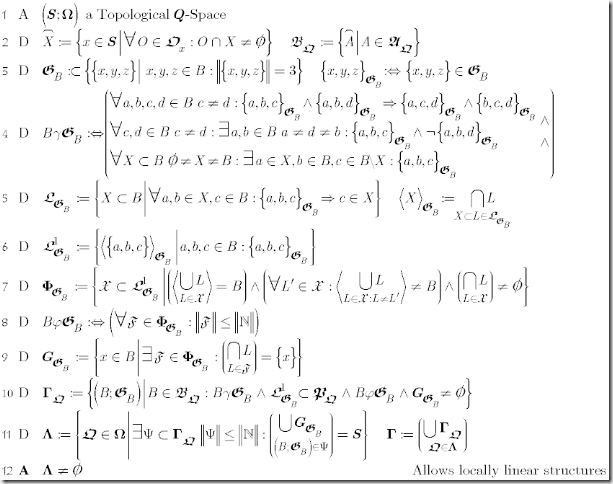
(1) As before, take Topological Q-Spaces as departing point. (2) As before introduces the topological closure and the closed hull of Alexandrov-Sets (=Double Cones) as base-set.
(3) However defines G as a strictly local relations within a base-set.
(4) Define 3 properties required to make G a useful Local Linear Structure:
(4.1) may be called the line property: 2 points define a line i.e. if two different points c and d are collinear to the same points a and b, then they are on the same line.
(4.2) may be called the separation property: different points differ in at least one line.
(4.3) may be called the connectivity property: it’s possible to get from anywhere to anywhere in a final number of linear steps.
The combination of (4.1) and (4.2) imply that locally G satisfies the axioms for Incidence geometry: all lines have at least 2 points, two points define exactly one line and finally any 2 different points are on at least 2 different lines, in our case even stronger: 2 different lines with each at least 3 points.
(5) defines linear sets i.e. those that with any 2 points contain all locally collinear points. The <linear set generated by a set of points> is the smallest linear set that contains them all. The concept of a generated linear set allows to introduce a combinatorial concept of linear independence.
(6) introduces the set of 1-dimensional linear sets or lines.
(7) defines a set of Frames i.e. minimal subsets of mutually linear independent lines (7.2), which generate the whole set (7.1) and are fixed at some point (7.3).
(8) Is a later required technicality: a Frame should be countable at least.
(9) singles out the anchor-points for Frames.
(10) defines for a Q-Order a Locally Linear Structure (though without metric part yet): all those pairs of a base-set B and a relation G defined on B such that it defines a linear structure on B (10.1), every line is at the same time a path in the underlying topology (10.2), all frames are at least countable (10.3) and finally there is at least one anchor point (10.4). Please note that there might be more but only one G i.e. the same base-set may carry more but one linear structure. Finally a Locally Linear Structure is a topological invariant, as a local homeomorphism takes lines to lines (consequence of 10.2).
(11) Selects all those Q-Orders for which there is a corresponding LLS such that there is a countable subset, whose anchor-points cover the whole set. The final LLS is just the union of LLS for all Q-orders.
(12) Just claims that there are Q-Orders with a Locally Linear Structure

Going back to Normal Neighborhoods of Lorentz-Manifolds. These are defined by selecting first one anchor-point (in the Einstein-concept the famous free-falling-observer). All points in a Normal Neighborhood of this anchor-point are connected by at most one geodesic, whence different points differ at least in one geodesic. All points connect by means of a geodesic to the anchor-point, and finally there is at least one frame –the normal coordinate system at the anchor-point- that generates the whole set. Obviously lines are paths in the underlying topology. Finally there is a Normal Neighborhood for any point. The dimension (8) for Frames is just 4. And the second-countability for Lorentz-Manifolds implies the countability restriction in (11)
Voilá exactly what the axiom-set 3 claims for Linear Q-orders.

Next step will be to explore the combinatorial elements of connections when expressed as mappings of frame-sets.

Combinatorial Pre-Weyl-Spaces

Introduction

We are looking for a combinatorial framework that, in an essential way, includes the structure of Space-Time as a continuous model on one side and the structure of of Petri-Nets as a finite (countable) model on the other.

Essential means that physically different Space-Times and logically different Petri-Nets shall have different models and that different models produce different Space-Times and different Petri-Nets respectively.

A wrong way to get time & space would be simply to assume them, as Einstein showed convincingly more but a century ago, refuting thereby Immanuel Kant, who another century before had declared time & space as logical “a priori” beyond material experience.
{Here and later on we will use deliberately time-space instead of the usual space-time when referring to our model}.

There is a second caveat already raised by Einstein –see The Challenge-:
At the very end, all measurement (and hence all Physics) boils down to have/to observe the coincidence of something at the same time-space point, while the description of time-space points using coordinates is just a convenient means to describe these coincidences.  Hence it should make no difference in the description at least, if another such system of coordinates is used, if only there is a one-to-one correspondence between the former and the latter.

Though a specific time & space may be extremely practical for a description and hence a necessary heuristic tool -among other to detect symmetries which reflect physical invariants-, the Physics described should not depend on the specifics of the used space & time: Any time & space should do, as long it produces the same pattern of coincidence.

The principle of General Covariance, even more its expression as diffeomorphism covariance, is for Einstein a sequitur of the idea of background independence. Actually he uses –and others since- nonetheless only these very specific coordinate-systems, those which are appropriate for the description of Differential Manifolds. Yet he never stated anywhere that the realm of Differential Manifolds would be for him the only domain for admissible Coordinate-Systems. 

Phrased more general by Fotini Markopoulou[1] : Background independence I (BI-I): A theory is background independent if its basic quantities and concepts do not presuppose the existence of a background space-time metric. Hence one might  argue that using Differential Manifolds as basic framework as such violates the background-independence postulate: the concept Manifold as such uses by its very definition at least locally always the Euclidian metric, not to mentioned that Topological Manifolds with 4 or more dimensions may carry more but only one Differential Structure, such that the very construction of the Riemann Curvature Tensor depends on a choice made before.

Following ideas already touched by Hermann Weyl[2] and resumed later by John Stachel[3], the Riemann Curvature Tensor can be decomposed in principally 2 different parts: a conformal part, which represents the causal structure, and a projective part, which represents the geometry of time-space. Both are usually defined on top of a suitable Differential Manifold, such that –including the latter- we have 3 basic structural ingredients.

Stachel observes that both the conformal and the projective part may be decomposed further, into a something completely combinatorial –the structures- and a something that provide measurement or metrics. In this way combining causal structure with volume or geometry with metric and applying suitable compatibly conditions, the original Riemann Curvature Tensor may be reconstructed.

A pure combinatorial, background independent approach hence would forget about inherent metrics and focus only on the combinatorial aspects of conformal and projective structure. Combinatorial models for geometry are known since the antique times, actually they were geometry until the 19th century.
Interesting enough, there is a very large class of purely combinatorial models for geometries –finite or discrete or continuous- which allows an algebraic representation by means of coordinates, something again that the ancient already knew about yet to its full extent was formalized not until the 19th and 20th century.  
For the conformal part we will present a combinatorial model for less restrictive than the normally used partial orders as it still allows time-loops.

Yet the underlying framework Differential Manifold itself comes with inherent metric properties twice. First it inherits topologic properties like regular and Haussdorff. which make the underlying topology metrizable. Second it inherits locally the Euclidean metric, which in turn is implicitly but intensively used in the Differential Calculi.  So for a pure combinatorial model we will have to drop some topological properties, while retaining what we think –from a combinatorial point of view- as essential.

Finally aiming “on long shot” on a Sum-over-history approach, we have to be aware that we will have to talk finally about not one but rather classes of causal structures and their respective probabilities.  Different causal structures may require different topologies, such that we will have to start with causal structures and introduce suitable topologies as an additional property. (In our last intent, we still started with topology and went from there to individual geometries and Q-orders).

[1]Fotini Markopoulou,Conserved quantities in background independent theories,Journal of Physics: Conference Series 67 (2007) 012019
[2] Hermann Weyl, Raum-Zeit-Materie, Julius Springer, Berlin 1919
[3] John Stachel, Projective and Conformal Structures in General Relativity, Loops ’07, Morelia June 25-30, 2007

The Axioms for Combinatorial Pre-Weyl-Spaces

The above sets the course for the following 3 sets of Axioms. The first set –Q-Spaces- defines Q-Orders as our representation for causal structures, i.e. the conformal part without metric. The second set –Topological Q-Spaces- constructs a topology based on Q-Orders and claims axiomatically two important topological properties of Topological Manifolds: being connected and being locally path connected. The third set –Geometric Q-Spaces- introduces local Incidence-Geometries as our model for the combinatorial aspects of the projective structure, sufficiently rich to be embedded point-wise into Projective Geometries.
The objects –sets and classes- defined by the 3 axiom-sets try to resemble the combinatorial qualities (or properties) of Pre-Weyl-spaces, i.e. the combination of a conformal and a projective combinatorial structure, yet without an equivalent for a connection nor any metric yet.

{Something about notation: we use pure Set-Theory, large letters denote sets, fractional large letters sets of sets and finally large Greek Letters sets of sets of sets. Bold letters are distinguished, named sets, which may be referenced later by their letter. Small letters denote elements of the base-set S. Except the usual letter (N) for natural numbers, there shouldn’t be any undefined name.
Sets are defined by denoting the element, sometimes giving the initial  originating domain (before |) and the condition a specific element satisfies (after |)
:= and :<> are used to introduce definitions: the left expression/symbol is defined by the right expression. The left side might be a predicate with arguments written as dyadic-operator (small Greek letter).
All and Existence quantifiers a represented a usual, with the element-variables before ‘:’ and the expression that combines the variables after “:”. Sometimes a restricting condition is included before “:”. Formulas with non-quantified element-variables carry an implicit All-quantifier at their beginning, ranging over the base set S.}

Axiom Set 1: Q-Spaces (a hint: by clicking opens another window with the formula-text in large).

(1) introduces the base-set S. (2) and (3) introduce the class of objects –Q-Orders- as subsets of pairs of pairs of distinct elements. (4) to (9) specify additional properties that we are demanding. The Q-relation resembles the ordering of 4 elements “on a path”.
(4) defines a predicate θ, true if the structure behaves like we assume it does (i.e. like a path). (The entry Going around in Circles I explores its meaning).
(5) is just a simplification of the Q-Relation: We forget the order and only remember that the 4 elements are on some path.
(6) Defines as predicate a rule of interference to combine different paths.  
(6.1) whenever all pairs of 3 points can be found on some path –regardless their configuration there-, there should be a 4th element giving some path, where all 4 may be positioned.
(6.2) whenever all triplets of 4 points are on some path, the 4 points themselves may be positioned on a path.. (The entry Going around in Circles II provides some heuristics for this rule and shows its consequences).
(7) defines as predicate τ a rule for separation and a rule for connectivity:
(7.1) requires that different elements may be separated by the Q-Relation. Be aware that only in the 1-dimensional case this implies that between any 2 elements there is a third one.
(7.2) enables to go from a subset to its complement just by interchanging one element. It forces S to have at least 5 elements.
(8) introduces the concept of double-cover to define in (9) a predicate ο that claims the existence of an global orientation.  4 points on a path may be traversed just in one of 2 cyclic directions, clockwise or counterclockwise. (9) extends this concept to whole Q respectively S. (The entry Going around in Circles III provides some heuristics).
(10) defines the class Θ of all Q-Orders on S that is of all sets Q that satisfy the axioms defined as predicates in (4), (6), (7) and (9).
(11) finally claims that Θ shall not be empty, i.e. S shall allow at least one Q-Order.

Notes: in Q-Spaces - Examples there are examples of Q-Spaces just with one Q-Order shown/defined. The entry as such still awaits its update to our most recent version. Yet for those familiar with causal structures on Lorentz-Manifolds: think about the Q-Order as the arrangement of for 4 points on a time-like curve …. and it becomes quite plausible that time-orientable Lorentz-Manifolds are indeed Q-spaces. A formal proof is still due.

Axiom Set 2: Topological Q-Spaces

As next step we will construct topologies from Q-Orders.
(1) defines a Q-Space as starting point. Be aware that Θ is a class of Q-Orders, hence (2) to (8) apply to members of this class (or are parameterized by its members).
(2) defines the set of Alexandrov-sets for a given Q-Order, i.e. all elements that are at one side between 2 points a and b, including the end points. These sets resemble the Alexandrov-topology for Lorentzian Manifolds.
(3) specializes the relation “be element of” into “be contained in” i.e. not only the element is element but there is a “left” and “right” neighbor.
(4) singles out Places among the elements of S: whenever a place is contained in two different A-sets, there is a third A-set containing the place and contained in the intersection of both. As heuristics, think about A-sets as neighborhoods, then the intersection of any two neighborhoods of a place contains a neighborhood for that place.
(5) With Places singled out, we define straight forward a topology O. The Open Sets for this topology are all those sets which for all their places contain a containing A-set. No proof needed to see that arbitrary joins of Open Sets and the intersection of two Open sets are open.
(6) defines a connectivity-predicate ω, true if a set can not be split into to two open, disjoint subsets i.e. this set is topologically connected.
(7) introduce the combinatorial equivalent of a Jordan-Curve, normally defined as the injective, continuous mapping of a circle, yet as injective carries the Hausdorff-property to the target-space, not applicable in our case. We define Paths as those connected subsets, which fall apart removing one element except at most 2, the possible endpoints.
(8) defines a stronger connectivity-predicate ω, true if any subset of a set and its complement can be connected by a path.
(9) selects into the class Ω all those Q-Orders from Θ that define a connected and locally path connected A-topology.
(10) finally claims that Ω shall not be empty, i.e. S shall allow at least one topological Q-Order.

Notes: All examples are topological Q-Spaces. In the discrete case, refining the A-Topology into the Path- or Hawking-topology, Q-Spaces turn out to be Petri-Nets. Finally, a topological manifold by definition is connected and locally path-connected. Yet only with additional constraints –for instance strongly casual- this topology and our A-Topology for Lorentz-Manifolds are equivalent. The exact investigation of these constraints for Q-Spaces has yet to be done.

Axiom Set 3: Geometric Q-Spaces

(1) defines a topological Q-Space as starting point. Be aware that Ω is a class of Q-Orders, hence (2) to (8) apply to members of this class (or are parameterized by its members). Please note that G is a global relation, even if we define its additional properties locally. This ensure that a property existing in on block remains valid in other blocks, which contain the same points.
(2) introduces the well know closure of a set and the closured A-sets as building-Blocks.
(3) introduces the objects or relations, we will use: subsets of the set of sets with 3 distinct elements.
(4) defines as predicate γ three properties, we will require locally i.e. within a block B.
(4.1) may be called the line property: 2 points define a line i.e. if two different points c and d are collinear to the same points a and b, then they are on the same line.
(4.2) may be called the separation property: different points differ in at least one line.
(4.3) may be called the continuity property: if there is a collinear third point anywhere, than there is a local representative.
The combination of (4.1) and (4.2) imply that locally G satisfies the axioms for Incidence geometry: all lines have at least 2 points, two points define exactly one line and finally any 2 different points are on at least 2 different lines, in our case even stronger: 2 different lines with each at least 3 points.
(5) defines linear sets i.e. those that with any 2 points contain all locally collinear point. The <linear set generated by a set of points> is the smallest linear set that contains them all. The concept of a generated linear set will allow later to introduce combinatorial the concept of linear independence.
(6) introduces the set of 1-dimensional linear sets or lines and the subset of those lines that go through a single point, some times called the star belonging to a point.
(7) the predicate λ transcribed literally claims that the star of any point contains an at most countable subset of lines whose points generate the whole block.
As for its heuristics, assume that a block carries an Euclidian geometry with finite dimension, then at each point one may find a finite number of lines that may serve as coordinates taking that point as origin i.e. generate the whole block starting at that point. More general, assume that a block carries the geometry resulting from separable linear vector-space, then at each point we may find a countable base for that vector-space. 
Different to the above examples, we still do not specify the procedure of how to reconstruct the whole block just starting from coordinates at a specific point. We only claim that these coordinates exist, what ever the procedure might be to generate the whole block.
Reversely, as all points are in this respect equivalent, moving from one point to another means changing the set of coordinates, or more precisely changing sets of coordinates at the origin by sets of coordinates at the destiny, as there might be more than one set at each point, procedures similar to those used when working with frame-bundles, yet again we still do not specify how-to.  
(8) introduces as predicate κ a simple compatibility condition between underlying Q-Order and Geometry: if a line contains 2 Q-related elements, then the whole line is part of Q, heuristically a time-like geodesic somewhere stays time-like all the way.
(9) defines the class Γ of all G-orders, for which there exists a Q-Order such that the axioms defined as predicates in (4), (7) and (8) are satisfied.
(10) finally claims that Γ shall not be empty, i.e. S shall allow at least one topological Q-Order and one complying G-order or Geometry.

Notes: with respect to Lorentz-manifolds, the normal or geodesic coordinates  define a Geometry  in the above sense, taking as blocks the closure of a totally normal neighborhood, in which any two points are connected be a geodesic. 3 points on such a geodesic from a g-triple {a,b,c}. The formal proof is still outstanding. Yet it appears as if all Lorentz-Manifolds are Geometric Q-Spaces. For Petri-Nets I have not found a concept similar to Geometry beyond the example Petri uses –the 2 dimensional Grid as combinatorial equivalent for an 2-dimensional Minkowski space. Yet in Minkowski-Space all and every thing is linear and in 2 dimensions there isn't a true conformal structure beyond triviality either (conformally flat).

Well, there is a lot still missing namely the definition of connections -that is the actual procedure or mapping when moving from point to point-, as the proper embedding of stars into Projective Geometries alas Vector-spaces, which will be required to define metrics and connections.

Again the examples appear to be valid even though I haven't revised them already one by one. Interesting the geometry for Génesis is the smallest Geometry possible .. and it’s most logical projective embedding appears to be the Fano-Plane, the smallest possible Projective Geometry.