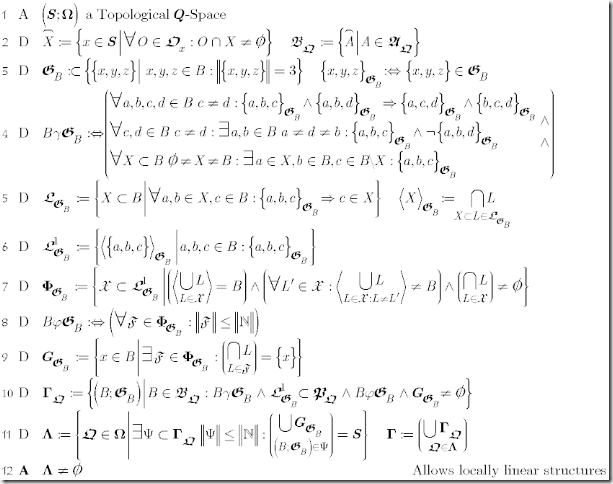Introduction
We are looking for a combinatorial framework that, in an essential way, includes the structure of Space-Time as a continuous model on one side and the structure of of Petri-Nets as a finite (countable) model on the other.
Essential means that physically different Space-Times and logically different Petri-Nets shall have different models and that different models produce different Space-Times and different Petri-Nets respectively.
A wrong way to get time & space would be simply to assume them, as Einstein showed convincingly more but a century ago, refuting thereby Immanuel Kant, who another century before had declared time & space as logical “a priori” beyond material experience.
{Here and later on we will use deliberately time-space instead of the usual space-time when referring to our model}.
There is a second caveat already raised by Einstein –see The Challenge-:
At the very end, all measurement (and hence all Physics) boils down to have/to observe the coincidence of something at the same time-space point, while the description of time-space points using coordinates is just a convenient means to describe these coincidences. Hence it should make no difference in the description at least, if another such system of coordinates is used, if only there is a one-to-one correspondence between the former and the latter.
Though a specific time & space may be extremely practical for a description and hence a necessary heuristic tool -among other to detect symmetries which reflect physical invariants-, the Physics described should not depend on the specifics of the used space & time: Any time & space should do, as long it produces the same pattern of coincidence.
The principle of General Covariance, even more its expression as diffeomorphism covariance, is for Einstein a sequitur of the idea of background independence. Actually he uses –and others since- nonetheless only these very specific coordinate-systems, those which are appropriate for the description of Differential Manifolds. Yet he never stated anywhere that the realm of Differential Manifolds would be for him the only domain for admissible Coordinate-Systems.
Phrased more general by Fotini Markopoulou[1] : Background independence I (BI-I): A theory is background independent if its basic quantities and concepts do not presuppose the existence of a background space-time metric. Hence one might argue that using Differential Manifolds as basic framework as such violates the background-independence postulate: the concept Manifold as such uses by its very definition at least locally always the Euclidian metric, not to mentioned that Topological Manifolds with 4 or more dimensions may carry more but only one Differential Structure, such that the very construction of the Riemann Curvature Tensor depends on a choice made before.
Following ideas already touched by Hermann Weyl[2] and resumed later by John Stachel[3], the Riemann Curvature Tensor can be decomposed in principally 2 different parts: a conformal part, which represents the causal structure, and a projective part, which represents the geometry of time-space. Both are usually defined on top of a suitable Differential Manifold, such that –including the latter- we have 3 basic structural ingredients.
Stachel observes that both the conformal and the projective part may be decomposed further, into a something completely combinatorial –the structures- and a something that provide measurement or metrics. In this way combining causal structure with volume or geometry with metric and applying suitable compatibly conditions, the original Riemann Curvature Tensor may be reconstructed.
A pure combinatorial, background independent approach hence would forget about inherent metrics and focus only on the combinatorial aspects of conformal and projective structure. Combinatorial models for geometry are known since the antique times, actually they were geometry until the 19th century.
Interesting enough, there is a very large class of purely combinatorial models for geometries –finite or discrete or continuous- which allows an algebraic representation by means of coordinates, something again that the ancient already knew about yet to its full extent was formalized not until the 19th and 20th century.
For the conformal part we will present a combinatorial model for less restrictive than the normally used partial orders as it still allows time-loops.
Yet the underlying framework Differential Manifold itself comes with inherent metric properties twice. First it inherits topologic properties like regular and Haussdorff. which make the underlying topology metrizable. Second it inherits locally the Euclidean metric, which in turn is implicitly but intensively used in the Differential Calculi. So for a pure combinatorial model we will have to drop some topological properties, while retaining what we think –from a combinatorial point of view- as essential.
Finally aiming “on long shot” on a Sum-over-history approach, we have to be aware that we will have to talk finally about not one but rather classes of causal structures and their respective probabilities. Different causal structures may require different topologies, such that we will have to start with causal structures and introduce suitable topologies as an additional property. (In our last intent, we still started with topology and went from there to individual geometries and Q-orders).
[1]Fotini Markopoulou,Conserved quantities in background independent theories,Journal of Physics: Conference Series 67 (2007) 012019
[2] Hermann Weyl, Raum-Zeit-Materie, Julius Springer, Berlin 1919
[3] John Stachel, Projective and Conformal Structures in General Relativity, Loops ’07, Morelia June 25-30, 2007
The Axioms for Combinatorial Pre-Weyl-Spaces
The above sets the course for the following 3 sets of Axioms. The first set –Q-Spaces- defines Q-Orders as our representation for causal structures, i.e. the conformal part without metric. The second set –Topological Q-Spaces- constructs a topology based on Q-Orders and claims axiomatically two important topological properties of Topological Manifolds: being connected and being locally path connected. The third set –Geometric Q-Spaces- introduces local Incidence-Geometries as our model for the combinatorial aspects of the projective structure, sufficiently rich to be embedded point-wise into Projective Geometries.
The objects –sets and classes- defined by the 3 axiom-sets try to resemble the combinatorial qualities (or properties) of Pre-Weyl-spaces, i.e. the combination of a conformal and a projective combinatorial structure, yet without an equivalent for a connection nor any metric yet.
{Something about notation: we use pure Set-Theory, large letters denote sets, fractional large letters sets of sets and finally large Greek Letters sets of sets of sets. Bold letters are distinguished, named sets, which may be referenced later by their letter. Small letters denote elements of the base-set S. Except the usual letter (N) for natural numbers, there shouldn’t be any undefined name.
Sets are defined by denoting the element, sometimes giving the initial originating domain (before |) and the condition a specific element satisfies (after |)
:= and :<> are used to introduce definitions: the left expression/symbol is defined by the right expression. The left side might be a predicate with arguments written as dyadic-operator (small Greek letter).
All and Existence quantifiers a represented a usual, with the element-variables before ‘:’ and the expression that combines the variables after “:”. Sometimes a restricting condition is included before “:”. Formulas with non-quantified element-variables carry an implicit All-quantifier at their beginning, ranging over the base set S.}
Axiom Set 1: Q-Spaces  (a hint: by clicking opens another window with the formula-text in large).
(a hint: by clicking opens another window with the formula-text in large).
(1) introduces the base-set S. (2) and (3) introduce the class of objects –Q-Orders- as subsets of pairs of pairs of distinct elements. (4) to (9) specify additional properties that we are demanding. The Q-relation resembles the ordering of 4 elements “on a path”.
(4) defines a predicate θ, true if the structure behaves like we assume it does (i.e. like a path). (The entry Going around in Circles I explores its meaning).
(5) is just a simplification of the Q-Relation: We forget the order and only remember that the 4 elements are on some path.
(6) Defines as predicate a rule of interference to combine different paths.
(6.1) whenever all pairs of 3 points can be found on some path –regardless their configuration there-, there should be a 4th element giving some path, where all 4 may be positioned.
(6.2) whenever all triplets of 4 points are on some path, the 4 points themselves may be positioned on a path.. (The entry Going around in Circles II provides some heuristics for this rule and shows its consequences).
(7) defines as predicate τ a rule for separation and a rule for connectivity:
(7.1) requires that different elements may be separated by the Q-Relation. Be aware that only in the 1-dimensional case this implies that between any 2 elements there is a third one.
(7.2) enables to go from a subset to its complement just by interchanging one element. It forces S to have at least 5 elements.
(8) introduces the concept of double-cover to define in (9) a predicate ο that claims the existence of an global orientation. 4 points on a path may be traversed just in one of 2 cyclic directions, clockwise or counterclockwise. (9) extends this concept to whole Q respectively S. (The entry Going around in Circles III provides some heuristics).
(10) defines the class Θ of all Q-Orders on S that is of all sets Q that satisfy the axioms defined as predicates in (4), (6), (7) and (9).
(11) finally claims that Θ shall not be empty, i.e. S shall allow at least one Q-Order.
Notes: in Q-Spaces - Examples there are examples of Q-Spaces just with one Q-Order shown/defined. The entry as such still awaits its update to our most recent version. Yet for those familiar with causal structures on Lorentz-Manifolds: think about the Q-Order as the arrangement of for 4 points on a time-like curve …. and it becomes quite plausible that time-orientable Lorentz-Manifolds are indeed Q-spaces. A formal proof is still due.
Axiom Set 2: Topological Q-Spaces 
As next step we will construct topologies from Q-Orders.
(1) defines a Q-Space as starting point. Be aware that Θ is a class of Q-Orders, hence (2) to (8) apply to members of this class (or are parameterized by its members).
(2) defines the set of Alexandrov-sets for a given Q-Order, i.e. all elements that are at one side between 2 points a and b, including the end points. These sets resemble the Alexandrov-topology for Lorentzian Manifolds.
(3) specializes the relation “be element of” into “be contained in” i.e. not only the element is element but there is a “left” and “right” neighbor.
(4) singles out Places among the elements of S: whenever a place is contained in two different A-sets, there is a third A-set containing the place and contained in the intersection of both. As heuristics, think about A-sets as neighborhoods, then the intersection of any two neighborhoods of a place contains a neighborhood for that place.
(5) With Places singled out, we define straight forward a topology O. The Open Sets for this topology are all those sets which for all their places contain a containing A-set. No proof needed to see that arbitrary joins of Open Sets and the intersection of two Open sets are open.
(6) defines a connectivity-predicate ω, true if a set can not be split into to two open, disjoint subsets i.e. this set is topologically connected.
(7) introduce the combinatorial equivalent of a Jordan-Curve, normally defined as the injective, continuous mapping of a circle, yet as injective carries the Hausdorff-property to the target-space, not applicable in our case. We define Paths as those connected subsets, which fall apart removing one element except at most 2, the possible endpoints.
(8) defines a stronger connectivity-predicate ω, true if any subset of a set and its complement can be connected by a path.
(9) selects into the class Ω all those Q-Orders from Θ that define a connected and locally path connected A-topology.
(10) finally claims that Ω shall not be empty, i.e. S shall allow at least one topological Q-Order.
Notes: All examples are topological Q-Spaces. In the discrete case, refining the A-Topology into the Path- or Hawking-topology, Q-Spaces turn out to be Petri-Nets. Finally, a topological manifold by definition is connected and locally path-connected. Yet only with additional constraints –for instance strongly casual- this topology and our A-Topology for Lorentz-Manifolds are equivalent. The exact investigation of these constraints for Q-Spaces has yet to be done.
Axiom Set 3: Geometric Q-Spaces 
(1) defines a topological Q-Space as starting point. Be aware that Ω is a class of Q-Orders, hence (2) to (8) apply to members of this class (or are parameterized by its members). Please note that G is a global relation, even if we define its additional properties locally. This ensure that a property existing in on block remains valid in other blocks, which contain the same points.
(2) introduces the well know closure of a set and the closured A-sets as building-Blocks.
(3) introduces the objects or relations, we will use: subsets of the set of sets with 3 distinct elements.
(4) defines as predicate γ three properties, we will require locally i.e. within a block B.
(4.1) may be called the line property: 2 points define a line i.e. if two different points c and d are collinear to the same points a and b, then they are on the same line.
(4.2) may be called the separation property: different points differ in at least one line.
(4.3) may be called the continuity property: if there is a collinear third point anywhere, than there is a local representative.
The combination of (4.1) and (4.2) imply that locally G satisfies the axioms for Incidence geometry: all lines have at least 2 points, two points define exactly one line and finally any 2 different points are on at least 2 different lines, in our case even stronger: 2 different lines with each at least 3 points.
(5) defines linear sets i.e. those that with any 2 points contain all locally collinear point. The <linear set generated by a set of points> is the smallest linear set that contains them all. The concept of a generated linear set will allow later to introduce combinatorial the concept of linear independence.
(6) introduces the set of 1-dimensional linear sets or lines and the subset of those lines that go through a single point, some times called the star belonging to a point.
(7) the predicate λ transcribed literally claims that the star of any point contains an at most countable subset of lines whose points generate the whole block.
As for its heuristics, assume that a block carries an Euclidian geometry with finite dimension, then at each point one may find a finite number of lines that may serve as coordinates taking that point as origin i.e. generate the whole block starting at that point. More general, assume that a block carries the geometry resulting from separable linear vector-space, then at each point we may find a countable base for that vector-space.
Different to the above examples, we still do not specify the procedure of how to reconstruct the whole block just starting from coordinates at a specific point. We only claim that these coordinates exist, what ever the procedure might be to generate the whole block.
Reversely, as all points are in this respect equivalent, moving from one point to another means changing the set of coordinates, or more precisely changing sets of coordinates at the origin by sets of coordinates at the destiny, as there might be more than one set at each point, procedures similar to those used when working with frame-bundles, yet again we still do not specify how-to.
(8) introduces as predicate κ a simple compatibility condition between underlying Q-Order and Geometry: if a line contains 2 Q-related elements, then the whole line is part of Q, heuristically a time-like geodesic somewhere stays time-like all the way.
(9) defines the class Γ of all G-orders, for which there exists a Q-Order such that the axioms defined as predicates in (4), (7) and (8) are satisfied.
(10) finally claims that Γ shall not be empty, i.e. S shall allow at least one topological Q-Order and one complying G-order or Geometry.
Notes: with respect to Lorentz-manifolds, the normal or geodesic coordinates define a Geometry in the above sense, taking as blocks the closure of a totally normal neighborhood, in which any two points are connected be a geodesic. 3 points on such a geodesic from a g-triple {a,b,c}. The formal proof is still outstanding. Yet it appears as if all Lorentz-Manifolds are Geometric Q-Spaces. For Petri-Nets I have not found a concept similar to Geometry beyond the example Petri uses –the 2 dimensional Grid as combinatorial equivalent for an 2-dimensional Minkowski space. Yet in Minkowski-Space all and every thing is linear and in 2 dimensions there isn't a true conformal structure beyond triviality either (conformally flat).
Well, there is a lot still missing namely the definition of connections -that is the actual procedure or mapping when moving from point to point-, as the proper embedding of stars into Projective Geometries alas Vector-spaces, which will be required to define metrics and connections.
Again the examples appear to be valid even though I haven't revised them already one by one. Interesting the geometry for Génesis is the smallest Geometry possible .. and it’s most logical projective embedding appears to be the Fano-Plane, the smallest possible Projective Geometry.