More –this time mathematical- heuristics

Let me try to explain what I’m trying to do. [Especially not trying to re-invent the wheel when there are so many proven, useful models at hand].

I’m aiming at Combinatorial General Relativity, as Einstein mentioned at the end of some of his writings as an unsolved puzzle.

Yet “my way” is not the usual top-down –i.e. trying to find quantization-rules on the very top- but “bottom-up” that is investigating in a more or less systematic fashion the implicit and explicit combinatorial elements and structures on each level. Here “causal structure”, based on the work of Stephen Hawking, David Malament and others, is already an almost closed chapter (Q-Orders).

The current “target”: differential manifolds.

Usually a manifold is defined using local homeomorphism between some local neighbor-hoods in the manifold-topology and some local part of a Euclidean space. For the latter normally one uses its algebraic definition (module over some field), gets from there to the usual Euclidean metric and then obtains the topology.

Now there is a completely equivalent set of Axioms for Euclidean Geometries: the famous Hilbert Axioms. Why would one like to use this set? Well, it’s known that there are finite, discrete models that satisfy the first set of Hilbert-Axioms (incidence Axioms for points, lines and planes), yet do not satisfy the second set (Order-Axioms) nor the third (Congruence-Axioms) and where the forth (Parallel-Axiom) is optional.

Not only this, but as v. Staudte, Moufang, Veblen, v. Neumann and others have shown, already the first set allows the construction of coordinates and hence metric, i.e. coordinates and metric arise using incidence relations and nothing else. [And that’s what I understand Einstein had in mind with his remarks].

Incidence relations as “founding ground” have a second great advantage: topological homeomorphisms carry them over automatically, i.e. suitably defined the manifold inherits these relations automatically, while congruence-relations or algebraic properties do not.

The “missing link”: Hilbert takes “lines” and “planes” as primitives (as does synthetic Geometry). So in my next –failed- intent I was looking where to find “lines” and “planes” in the context of Riemann and Pseudo-Riemann manifolds, and voilá there they were: geodesics and totally normal neighborhoods, yet with a tremendous drawback: their definition already requires concepts of the very, very top like the metric-tensor and the exponential map.

So I did a step backward, asking myself: is it possible to introduce lines using ONLY topological concepts? The model at hand: balls and spheres as defined by the usual Euclidean metric.

Next step: is it possible to define balls and spheres without using metric? Well it is. One might use simply connected neighborhoods and simply connected surfaces and, as recently shown, we get nice spheres in all dimensions.

Problem: “simply connected” as concept requires Hausdorff-spaces and imports via Homotopy the whole “World of Reals”, incompatible with my aim to allow also discrete, finite models not talk about my suspicion that it is a far to restrictive assumption for the real World (there are holes almost everywhere). Therefore I replaced “simply connected” by just “locally path connected”.

Next step: given sets of surfaces of locally path connected neighborhoods, what would be a minimal set of axioms based only on incidence and topology that would convert this set locally into something similar to the Euclidean Balls and –Spheres we started with? There a point lies on a straight line between two points iff there are Spheres for each of them that touch each other exactly in that point. More over the Spheres made using Euclidean Distance form a complete order around each point. There are additional compatibility rules among the spheres of different points on the same straight line. Finally “completeness” respectively “coherence” is to be considered i.e. in Euclidean Geometry there is always a straight line that connects them. This again would provoke “continuous models only” already in three dimensions. So I weakened this requirement to: “it should be possible to go from anywhere to anywhere in straight steps” and “if there are intersecting spheres for two points, then there are touching spheres (and hence a line that connects them)”.

Done this, we get a set of definitions invariant under any topological homeomorphism. That means two things: they carry over “automatically” to the manifold (locally of course), but second they produce a natural gauge. (Not such a surprise: there quite many metrics already for the real line, which produce the same topology. For instance the max-norm reproduces the same topology yet has cubes as balls).

Once I’ve got lines, the remainder is almost straight forward, using well known properties from synthetic geometry for triangles and quadrilaterals as axioms required to be able to “construct” coordinates and metrics. Yet (a) they all use nothing but incidence relations (b) are satisfied by usual Euclidean Geometries and therefore (c) inherited –locally- by any manifold.

Adding the additional structure of lines, adds to the compatibility-conditions for an Atlas of “charts with lines”. While the topological part remains –coincidence of topology on intersections-, I’m not yet finished of what is required in my case. [Again not such a surprise, taking into account that a Differential Manifold imposes additional compatibility conditions and that –exotic spheres from 4 dimensions onward- there might be more but only one Differential Structure].

Compatibility-Conditions and polish-up may still take some weeks or months, among other because I’m not sure whether going from “simply connected” to “locally path connected” is to weak, that is at least something similar to “star-connected” might be required (yet this as concept already uses “straight lines” so … ).

Topology and Geometry: Heuristics

This is yet another attempt to define and deduce the two very basic ingredients of the type of structures we would like to use as common underpinning for General Relativity Theory (normally assumed to be continuous) and General Net Theory (for which the so called Petri-Nets are just one example). This time we will concentrate on Topology and Geometry.
Be aware: this is work in progress!

III Geometry

I.0 Initial Heuristics

0.1 Einstein himself

EUCLIDEAN AND NON-EUCLIDEAN CONTINUUM
The surface of a marble table is spread out in front of me. I can get from any one point on this table to any other point by passing continuously from one point to a "neighboring" one, and repeating this process a (large) number of times, or, in other words, by going from point to point without executing “jumps". I am sure the reader will appreciate with sufficient clearness what I mean here by “neighboring" and by “jumps" (if he is not too pedantic). We express this property of the surface by describing the latter as a continuum.

Let us now imagine that a large number of little rods of equal length have been made, their lengths being small compared with the dimensions of the marble slab. When I say they are of equal length, I mean that one can be laid on any other without the ends overlapping. We next lay four of these little rods on the marble slab so that they constitute a quadrilateral figure (a square), the diagonals of which are equally long. To ensure the  equality of the diagonals, we make use of a little testing-rod. To this square we add similar ones, each of which has one rod in common with the first. We proceed in like manner with each of these squares until finally the whole marble slab is laid out with squares. The arrangement is such, that each side of a square belongs to two squares and each corner to four squares.

It is a veritable wonder that we can carry out this business without getting into the greatest difficulties. We only need to think of the following. If at any moment three squares meet at a corner, then two sides of the fourth square are already laid, and, as a consequence, the arrangement of the remaining two sides of the square is already completely determined. But I am now no longer able to adjust the quadrilateral so that its diagonals may be equal. If they are equal of their own accord,  then this is an especial favor of the marble slab and of the little rods, about which I can only be thankfully surprised. We must needs experience many such surprises if the construction is to be successful.

If everything has really gone smoothly, then I say that the points of the marble slab constitute a Euclidean continuum with respect to the little rod, which has been used as a “distance" (line-interval). By choosing one corner of a square as “origin", I can characterize every other corner of a square with reference to this origin by means of two numbers. I only need state how many rods I must pass over when, starting from the origin, I proceed towards the “right” and then “upwards”, in order to arrive at the corner of the square under consideration. These two numbers are then the “Cartesian coordinates" of this corner with reference to the “Cartesian coordinate system" which is determined by the arrangement of little rods.

By making use of the following modification of this abstract experiment, we recognize that there must also be cases in which the experiment would be unsuccessful. We shall suppose that the rods “expand" by an amount proportional to the increase of temperature. We heat the central part of the marble slab, but not the periphery, in which case two of our little rods can still be brought into coincidence at every position on the table. But our construction of squares must necessarily come into disorder during the heating, because the little rods on the central region of the table expand, whereas those on the outer part do not.

With reference to our little rods –defined as unit lengths- the marble slab is no longer a Euclidean continuum, and we are also no longer in the position of defining Cartesian coordinates directly with their aid, since the above construction can no longer be carried out. But since there are other things which are not in influenced in a similar manner to the little rods (or perhaps not at all) by the temperature of the table, it is possible quite naturally to maintain the point of view that the marble slab is a ”Euclidean continuum". This can be done in a satisfactory manner by making a more subtle stipulation about the measurement or the comparison of lengths.

But if rods of every kind (i.e. of every material) were to behave in the same way as regards the influence of temperature when they are on the variably heated marble slab, and if we had no other means of detecting the effect of temperature than the geometrical behavior of our rods in experiments analogous to the one described above, then our best plan would be to assign the distance one to two points on the slab, provided that the ends of one of our rods could be made to coincide with these
two points; for how else should we define the distance without our proceeding being in the highest measure grossly arbitrary?

The method of Cartesian coordinates must then be discarded, and replaced by another which does not assume the validity of Euclidean geometry for rigid bodies. The reader will notice that the situation depicted here corresponds to the one brought about by the general postulate of relativity.

Taken from:  Relativity: The Special and the General Theory, Pages 77-80, A Popular Exposition, 3rd ed. Author: Albert Einstein, Translator: Robert W. Lawson, retrieved from http://www.gutenberg.org/ebooks/36114)

0.2 Appreciation and Findings

Carefully reading the above, there are no numbers involved except counting and actually the whole configuration stays the same when applying heat somewhere, even if rods may need bending not only expansion and angels are no longer right ones. So at the very bottom Einstein talks about Topology and not Geometry, since the whole Geometric content reduces to certain configuration-sets –bended squares-that stay invariant under homeomorphisms.  Please note, that in Einstein's considerations there is explicit geometric content –the construction itself- and there is implicit geometric content, for instance the surprise that thinks workout so nicely or the assumption that rods represent somehow shortest connections.

The question hence is: can we express the above using only means of topology, that is converting the implicit assumptions into to properties of purely topologically defined configurations i.e. without referring to metrics, including angles? The answer is: Yes, we can. Before doing so within the framework of our Q-Topology, some additional Gedanken-experiments.

Einstein starts off with straight rods and squares constructed using the rods. Now straight is itself a concept deeply founded in Euclidian thinking as the shortest connection between to points. We now know, just thanks to General Relativity, that the straightest connection itself is defined by the curvature of space-time, hence not a very good starting point to define space-time. What about square? Well, actually Einstein does not use the whole square but rather only its border. And border is a topological concept. So let’s try what happens if we start with circles, assuming that we’ve got for each point a set of circles surrounding it.

Here we got some points scatter in a plane. Actually they were produced plotting for some points sets of circles surrounding these points, or more precisely some points of these circles.

 

 

 

 

 

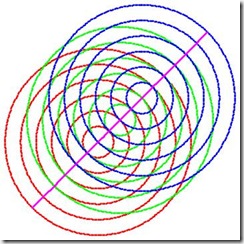
Here we have the same plane, yet for 3 points we added 4 circles for each and a straight line that runs through these 3 points. Did we just invent this line? No! If you look closer, wherever two different circles share just a single point, there goes the straight line. Or to put it differently, a third point is on a straight line between to other, if there is a circle for each of the 2 and these circle share exactly this third point. By tweaking Mathematica a little bit more, these 3 would have been part of the original set of scattered points.

Here the same picture without the clutter. There are more relations to discover: If a point is at the 1 point-intersection of two circles, then this point itself has two circles, which intersect exactly with one circle of one point and the other point. This means the relation for three points to be on one straight line is permutation invariant.

 

 

Here we added just a forth circle. As it appears, if two different points are each on a straight line with two other points, then all four are on the same line.
And: a point is just in the middle of two other points on the same line, if it has exactly 1 circle running through these 2 points, met a each by a circle from the opposite point.

And here we got a set of circles that is definitively off the line.
In the case of classical Euclidian Geometry, all the observed relations are easily proven. i.e. they are Theorems. But that’s not our interest here. The point is, that once established, they remain valid at least locally under continuous, bijective transformations, i.e. –topologically speaking homeomorphisms- as they preserve sets, intersections and borders, the only concepts we’ve used so far.

 

 

 

 

 

 

 

These are just two examples of different projections of the same configuration: tossing and stretching has no effect, even if our circles aren’t circles anymore.

 

However, we may not transform circles individually. Here the ellipsis  is the result of trying to transform individually the last circle and the result spells disaster. The ellipsis has still 1-point intersections with other circles yet somewhere else. Transformations therefore affect at least locally complete neighborhoods and we can not transform things nicely, i.e. if some borders are circles and others not, there is no transformation that would turn all at once into circles. 

 

 

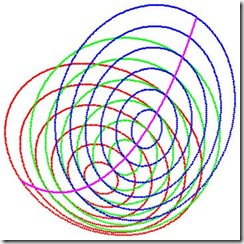
A final, drastic example: this transformation leaves the circle-sets as sets intact – each depicted in a different color-, yet suddenly our straight line isn’t straight anymore; well it depends: If we take Einstein and our above observations seriously –i.e. that a straight line is defined by its intersecting circle-sets, whatever these circles or equivalent descriptions may be, then the line is now as straight as it was before. We are just using a different but equivalent set of coordinates to describe the configuration or –what finally becomes the same- it’s the same configuration, only in a different gravitational field.

Now let’s see what happens if instead of circles or ellipses we use something else, for instances, as Einstein did, squares respectively quadrilaterals. Topologically speaking, that is without metrics, they are equivalent anyway.

Apparently in this example and it’s transformation, everything works fine. Yet the next example shows that we are in deep, deep trouble.

 

The straight line runs thru the lower right corner, the center and the upper left corner, yet the central quadrilateral though it touches upper and lower quadrilaterals, it does so not in a single point but in a whole segment.

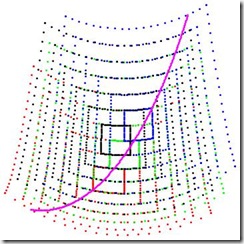
Gauss and Einstein would say: don’t worry! Just adapt and refine your grid and at the limit everything will be fine.  The next picture tries to illustrate this idea.

 

The smaller the quadrilaterals get, the smaller gets their intersection, which appears as if closing in on the line. Yet Heisenberg now would say: be aware, you can’t always refine to the limit, while Feynman would add: well any point of the segment of intersection is part of a possible shortest path, they just differ in their probabilities. The point with the highest probability will be the point closest to a straight line.  

The first approach assumes that somehow, at least in a small neighborhood, we would already know what straight line means, and then starting from there construct an appropriate grid. This would be in discordance with our whole approach, where we would like to use a given grid to define what straight line means.

The second approach requires tools ways beyond pure topology, and even then remains somewhat circular, as its requires already a metric to define the respective wave-functions, which in turn yield the probabilities, where we would like to deduce the metric using the grid and not use a metric to deduce the grid as peaks and lows of the probability function.

The critical condition, that could not be met easily nor always, was that two circles meet just in one single point. What if relaxing this condition just a little bit? To get a better idea, let’s have again a look on the offline circle, now an offline quadrilateral.

There are appearing differences: the green quadrilateral cuts segments out of blue and red, as they do with respect to green, likewise black cuts green and blue and they in turn cut black. Yet while the green-red and red-green respectively green-blue and blue-green segments are the same, the black-blue and blue-black respectively black-green and green-black segments differ; and that is a pure topological difference, which allows us the distinguish the configuration of black wrt.  blue and green  from the configuration of green wrt. red and blue.

For further considerations we will hence relax “share just one point” to “share just one segment”. As to end the heuristics part, we’ll have a look without further discussion on touching and intersecting spheres and cubes in 3 dimensions.