Going Backward, Going Forward – Part II

Partial obsolete – see below

This post will be dedicated to 1-dimensional Q-Orders, studying the effects Axiom 6 Q-Topology has on them and preparing the ground for the n+1-dimensional case.
Axiom 6
  

We will study 4 cases: the Rational Numbers, the Real Numbers, the Cyclic Group Zn and the Circle Group, using for the latter geometric representations on the Unit-Circle when appropriate.

Here are the more formal definitions:
Lemma F 6

The proof for F 6.2-3 –we assume the normal order <, was already given –they are as full orders also partial orders-, for F 6.7-8 the reader, if in doubt, is kindly invited to go back at least to Going in Circles – Part III. The constraints -Reduced, Regular, Q-Connectivity- are obviously satisfied.  

Obsolete by the Great Simplification … yet still useful for heuristics .. and will be replaced soon.

Next we will have a look on the corresponding Line-Sets.
Lemma F 7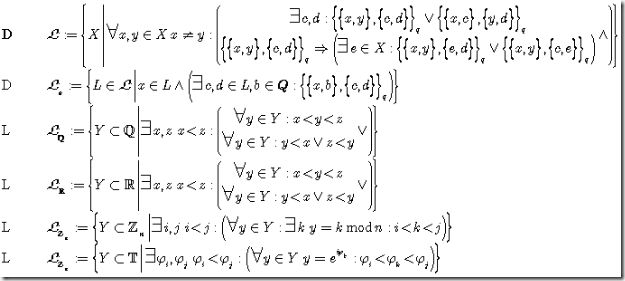

To show the intended above: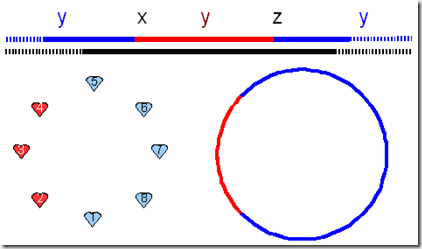
 
Please note that in all cases the red or blue marked sets designate or represent just one line, despite that apparently this line is not always connected.

Next we will look at l-closed points, and the open line-filter and open neighborhood-filter for each case.
Lemma F 8
As the definition for open L-intervals –hence the open neighborhood-filter- requires that only for l-closed points there is a surrounding L-interval, in case of Zn any interval is by definition open, as all points are open hence any neighbor-hood is open. Different in the other three cases.

Next a look on the topologies and whether they fit into Axiom 6. Nothing new, all rather very basics from elementary topology.
Lemma F 9 

No big surprises yet, as it is no surprise that Real Line and Circle Group both satisfy Axiom 6.7, mainly due to their Dedekind-Completeness.

This end our first round through 1-dimensional Q-Orders.