A Glimpse of the Big Picture

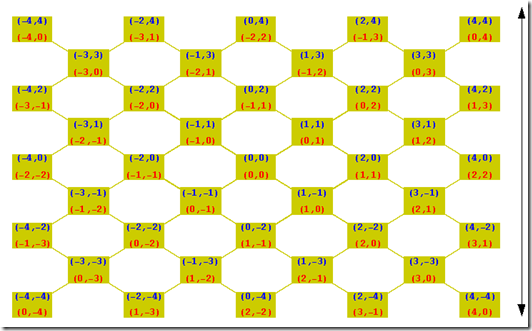
I’ve been asked whether there is a single text, that comprises the most essential of Q-Orders. Well – there is not, or not yet. To get an idea of what is and what not yet, may be the below picture helps.

The Big Picture

The left side shows in a very simplified manner the tower of mathematics beneath contemporary, classical General Relativity Theory. The right side, as far as I’m aware  less solidified and standardized yet, the tower of mathematics beneath contemporary usage of Petri-Nets in Informatics.

I had this picture already in my office about 30 years ago. Now, I thought, if one would like to relate seriously the truly interesting part on top of the left tower with something may be interesting on top of the right tower –meaning by proofs and not by analogies- then one would need a mathematical bridge between both towers, starting already on some quite low-level of both towers.  This is, where the work on Q-orders started. They should permit both types of domains –Real and Countable- and should produce one single category of a topology to relate both towers.

To complicate the issue, I discarded partial orders as the funding concepts, as both from Physics and Net-Theory we knew that it are the cycles, that produce basic invariants, on the very end even enable measurement: while we can measure our time as cycles, we can’t measure space without using time. [I know Carlo Rovelli will most strongly disagree].

I did know already the red elements towards the center, they were developed while I was still a GMD. 10 years later, Olaf Kummer and  Mark-Oliver Stehr (1) give a quite complete résumé of what has been found out. Yet –though published already in 1976- I was not aware of the proposal of Hawking et. al (1) for a New Topology for Space-Time, i.e. the blue elements towards the center.

May be if I’d known, my life’s history would have been different. Yet I did know already then that the basic invariant of embedding Petri-Nets into (1+n)-Vector Spaces seemed to be the group of conformal transformations. So after leaving GMD in 1985 I accumulated notes and proofs on predecessors for Q-Orders, yet without any serious break-through, still I succeeded giving Axioms 1-5 for Q-orders their current form. (See Going in Circles Part I to III).

After getting back more seriously, about in 2007 or so, and using the resource Internet (+some additional dollars, unfortunately many seminal papers are still sold, while they should be free for humanity), I got across the cited paper from Hawking and a later companion by David Malament (3). Suddenly there was a correspondence already worked-out: a structure on both sides, whose geometrical invariant is the conformal group.

So the only task remaining was to find an axiomatic definition for the Q-Topology, that covered both sides –the Hawking Topology and the Net Topology-. Yet Hawking and Malament use for definitions and proofs many features intrinsically related with lower parts of their tower, starting with the standard definition of paths, which carries automatically the Hausdorff-properties of Reals into the Topology to be defined, over concepts like locally convex, which make sense in a Real-Linear-Vector-Space setting, yet not in the right tower etc. etc. etc. So it took some time to get to the current axioms of Q-Topology (Axiom 6) and Q-Loop-Topology (Axiom 7), which both do only rely on concepts available on both sides of the Big Picture. (The trapped arrow of Time Part I-III).

So what is finished –at least in my electronic scrap-book- is the basic bridge. And I will continue to present its definition and related results during the next weeks. Specifically I will introduce a rich set of models, all by themselves important, for Q-Orders, which will construct something may be close to the fundaments for middle-tower that might be of some use by itself. Done, I’ll proceed to recompile the essays into one single paper, to be published may be through my arXiv account.

Yet I’m fully aware that there is still neither Informatics nor Physics in the picture, which both start on top of their respective towers. The fundamental problem: we have no tools yet to formulate equations or even quantify invariants. Though it’s known that the Hawking-Topology allows to reconstruct the metric and it’s known that the conformal group of transformation corresponds to a single central source of gravity, but as far as I know –and found googleing the Internet- nobody has investigate yet the full way back: i.e. given a Einstein (or Einstein-Cartan) field-equation and posing some reasonable constraints on its right –Energy-Tensor- side, what are the effects on the underlying Casual Structure? (Though Alfonso García-Parrado  and Miguel Sánchez (4) may give some hints).

As these tools are still missing, it doesn’t make much of sense either to speculate about the formal relations between the big tower underlying contemporary Quantum-Mechanics and the modest elements presented so far.

There is however the sketch of a work-program to complete and solidify the middle-tower, once finished the above presentation.  

1. Going downwards, it appears attractive to introduce the concept of a Q-Manifold. The Q-Manifold will be defined using the Complex or Quaternion (alas 2 and 4 dimensional Minkowski-Spaces) as base-space, using q-continuous functions instead of the usual Euclidian ones. The advantage: it appears as if a Q-Manifold is automatically smooth.
2. As defining measures on S1 is quite standard and the q-continuous images of S1 correspond to Q-Loops, it should be possible to get some notion of distance for Q-Loop-Spaces.
3. Similar remembering that the Tangent-Space may be defined as local equivalence classes of paths (alas Q-loops in our model), it should be possible to have a sort of Tangent-Space for Q-Loop-Spaces.

My only hope: my conditions of work will permit to continue … and the readers of this BLOG don’t get too impatient too soon as truly seminal posts are still month away.

The Axioms 
   

(1) Olaf Kummer, Mark-Oliver Stehr: Petri's Axioms of Concurrency - A Selection of Recent Results , Proceedings of the 18th International Conference on Application and Theory of Petri Nets, Toulouse, June 23-27, 1997, Lecture Notes in Computer Science 1248, © Springer-Verlag , 1997
(2) S. W. Hawking A.R. King and P. J. McCarthy, A new topology for curved space-time which incorporates the causal, differential and conformal structures Journal of Mathematical Physics Vol. 17, No 2, February 1976
(3) D. Malament, The class of continuous timelike curves determines the topology of spacetime Journal of Mathematical Physics, July 1977, Volume 18, Issue 7, pp. 1399-1404
(4) Alfonso García-Parrado, Miguel Sánchez,  Further properties of causal relationship: causal structure stability, new criteria for isocausality and counterexamples, arXiv:math-ph/0507014v2

The trapped Arrow of Time – Part I

Obsolete by the Great Simplification … yet still useful for heuristics

The Axioms 1-5 allow to speak about q-sets –our hammer- and points –our nails-, yet we don’t have a space where to put eventually constructed buildings –physical processes-.

The wrong way to get a space would be simply assume it, as Einstein showed convincingly a century ago refuting thereby Immanuel Kant, who another century before had declared space & time as logical aprioria beyond material experience.

There is a second caveat already raised by Einstein –see The Challenge-: though a specific space & time may be extremely practical for a description and hence a necessary heuristic tool, the Physics described should not depend on the specifics of the used space & time: Any space & time should do, as long it produces the same pattern of coincidence.

However –advancing results to be proven in later posts- some additional notes seem necessary:

• Einstein writes about point-events, where only point is the mathematical essence while event is already an interpretation, which apparently turned into a misleading trap for many, many, when they tried to identify the point-events of Einstein with quantum-leap-events from Quantum-Mechanics as introduced by Niels Bohr and Werner Heisenberg. At least I myself was caught in this trap until very recently, though Wolfgang Pauli –as I found out only after getting out of the trap- already noted in 1953 that this identification is false: due to the uncertainty principle QM-events can never ever correspond to closed GRT-points. This is a basic fact of physical life, by no means subject to, less result of impossibilities of observation, as what not is, can not be observed either, notwithstanding bad results from bad observations. It’s more over a structural property and not a consequence of erratic behavior of nature: we hold with Einstein God does not play dice.
• The principle of General Covariance, even more its expression as diffeomorphism covariance, is for Einstein a sequitur of the idea of background independence, yet he never stated anywhere that the realm of Differential Manifolds would be for him the only domain for admissible Coordinate-Systems. As long as we conserve the pattern of coincidence other Coordinate-Systems may do as well (and should do). We are about to show –even though we still have a long road ahead- that Q-Orders might be another, more general candidate.

There is another old saying The reinvention of the wheel results easier with a model at hand, so before continuing lets introduce a a model.

The above highly regular structure has two types of “points”, boxes and connectors. To illustrate Coordinate-Systems just as labels, we have labeled the boxes twice, once in blue, once in red, connectors in this simple model apparently need no own labels, as they can be uniquely identified by their limiting boxes. The arrow on the right indicates the possible directions.

Some q-set using red labels {{(0,-4),(0,-2)},{(0,-3) ,(0,-1)}}
The same using blue labels {{(-4,-4),(-2,-2)},{(-3,-3),(-1,-1)}}
A connector in red: {{(0,-4),(0,-1)},{{(0,-3) ,(0,-2)},(0,-5)}}
A connector in blue: {{(-4,-4),(-1,-1)},{{(-3,-3),(-2,-2)},(0,0)}}
Parts of a red line {{(m,2n),(m,2(n+1))},{(m,2n+1) ,(m,2(n+1)+1)}}
Parts of a blue wave {{(m,2n),(m,2(n+1))},{(m+1,2n+1),(m+1,2(n+1)+1)}}
… much more on this in a later post.

The shown grid may be considered as just a window to larger grid, that extends above and below, left and right, yet looking only on the window there is no way to tell whether the grid will extend to eternity respectively infinity or will bend somewhere, somehow returning into itself.

Final observation: take the grid as such, i.e. it’s located nowhere nor occupies anything else. Obviously its representation may need pixel on a screen, bits and bytes in some memory, ink and paper elsewhere, but all these representations, including those that use labels as their means of representation, are only shadows as Plato would have said of the idea grid.

Advancing in content, the picture may be considered as a window on a 2-dimensional discrete Minkowski-Space, once labeled as usual with a time- and a space-coordinate, once with mixed 2 space-time coordinates as first introduced by Kurt Gödel. In the latter form it’s also known as Petri-Grid, as it is a cornerstone in Carl Adam Petri’s General Net-Theory.

Please note that all this is until now pure interpretation of two, among many other, possible label-systems, yet as the labels considered as numbers may reflect in their arithmetic knowledge about the underlying structure, the above chosen labels seem to be useful, each for a different purpose.

Yet the picture has also another interpretation as the structure of an one-dimensional discrete Random Walk, which in turn is the discrete equivalent for the Diffusion-Equation.

Now this equation is the real counterpart to the one-dimensional imaginary Schrödinger-Equation, which models the 1 dimensional harmonic oscillator, whose solution-structure at minimal energy can be represented by Génesis (more about Génesis and Q-Orders).

Génesis is not only the smallest possible Q-Order, but also corresponds to the smallest possible folding of the above defined blue waves.

Hence if our Hauptvermutung is correct and all falls neatly more or less in its place, then the empty discrete 1-dimensional Minkowski-space is not empty at all, but rather constituted not filled by zero-point energy waves, just as it should be … but this nice result is still many, many posts away.

There is a third caveat, this time from Logic. Except Axiom 5, all preceding Axioms stayed within First Order Logic, i.e. referred to individual elements, not to properties of non-constructive sets (Obviously the domains (Q,Q) themselves are many times non-constructive). Though we used already Circle as a heuristic means, talking formally about the Geometry of Space & Time will require to talk formally about sets and their properties, relations among sets and their respective properties and finally functions and sets of functions and their properties.

And here we are in some very fundamental troubles for 2 reasons:

1. The risk of circular nonsense-definitions ala Bertrand Russell or the famous lying Cretans.
2. The almost theological decision to accept or not to accept the Axiom of Choice (or variants, like Zorn’s Lemma and others)

Well, with respect to the first we will stick to some typographic and definition-discipline to avoid –hopefully- trivial definition pitfalls, using different typos for different levels of classes:

1. Small letters for elements, CAPITAL letters for sets, two small letters (or more) for relations among elements.
   Bold letters refer to sets defined before, as we use one of the standard conventions to name Natural Numbers, Integer, Real, Complex and finally Quaternion (or Hamilton Numbers).
   Sometimes we use a subscript to indicate that the definition is to be understood as local i.e. as attached to some specified element(s).
2. Fraktur letters for Sets of Sets and their elements, hence in their definition (:=, :<=>) on the right side appear either sets of level 1 as elements or the elements are taken out of an already defined set of this level.
3. Greek Letters for Sets of Functions/Relations and their elements
4. Though we use recursive and implicit definition as a powerful tool, only primitive recursion is used (with a single, harmless exception sometimes: the implicit definition of equivalence classes).

There will be –maybe- a later post explaining in more detail the whole symbolic language, notation and logical mechanics used. Yet I fear that a 5 pages “must read first” primer about language and notation had been counterproductive. Therefore I hope that the actual snippets together with their verbal transliteration and picturesque illustration are sufficient to capture the intended meanings.

With respect to the second, we accept the Axiom of Choice, yet will try to avoid its usage whenever possible with reasonable effort or else raise the red flag.

This ends the long introduction for Axiom 6.

Going in Circles – Part III

There is an old saying When the only tool at hand is a hammer, the world appears to be a bunch of nails. Our hammer are the sets {{a,b},{c,d}}, the nails are the points, Axiom 5 defines then how the world appears to us.

Axiom 5 ORI Orientation

Axiom 5.3 is still quite easy to understand: it claims that the relation Q is connected by q-sets. Whatever cut into two pieces, there will be always 2 q-sets that differ only in 1 element to connect the pieces. This claim generalizes Q-Order Axiom 4 ORD as a careful inspection shows: the implications of Axiom 4 establish exactly this type of connection between their left and right sides.

Lemma A 9 shows that any two q-sets can be connected in a finite number of steps.

Lemma A 10 shows how this connectivity extends to Q: any two points are connected through a finite number of q-sets.

Hence our world is, as intended, connected only by hammers and nails. In a later post about Q-Topology we will see the equivalence to path-connected.

Now the harder parts of Axiom 5, which are intrinsically related to one of the most complicated problems in Algebraic Topology: the problems whether a space has a systematic orientation. In our case there is also a close, independent and direct relation to Group Theory. Both relations will be touched, maybe, in some later posts.

It should be mentioned that there have been related, relevant investigation also in the realm of Petri-Nets, e.g. the Orientation of Concurrency Structures by Olaf Kummer and Mark-Oliver Stehr(1), the Construction of globally Cyclic Orders by Stehr(2) and the proposal of cycloids as basic building blocks by Carl Adam Petri. Again these subjects will be touched, maybe, in a later post.

For our current purpose of motivation only, some picturesque considerations and some simple supporting lemma appear sufficient.

We know already that the points on any circle may be visited one after one in exactly two fashions or orientations: clockwise or counter-clockwise. And –as the following picture shows once more- interchanging (a,b) to (b,a) in {{a,b},{c,d}} reverses the direction.

Axiom 5.1 constructs first a set, a double-cover, that for each {{a,b},{c,d}} contains exactly two sets of sequences to run the circle, either clock- or counter-clockwise. We do not define which is which (same column = same orientation).

The idea of double-covers in Topology is to split the double-cover later into 2 subsets such that each original element has exactly 1 orientation, applying consistency rules to guarantee a orientation defined as uniform for all elements. From our experience with 5 points, we know it should be sufficient to have a consistency rule just for 5 points and then extend this rule. Let’s see.

Lemma A 2 tells us which are the q-sets for this configuration, which enables us to construct manually the double-cover and the desired single-covers .. to find the rule.
Lemma A 11
 

At this stage we know that to be consistently clockwise oriented all quintuples of 5 points must fit into the above definitions and that then the rule expressed as lemma holds.

Axiom 5.2 converts these findings for 5 points into a claim. We claim: there shall exist a split of the double-cover into two single-covers, such that the found rule holds for all quintuples in each of the single-covers. We define then that these Q allow a consistent orientation. Due to Axiom 5.3, there are exactly 2 possible global orientations. Therefore it’s sufficient to define the orientation for any {{a,b}},{{c,d}} to have it defined it for all Q or: there is only one direction of the arrow of time -even though it might be actually cyclic- and its orientation extends from anywhere to everywhere in finitely many steps.

Though somewhat surprising, it’s almost mathematical routine to convert a property found in a specific case into an axiomatic claim: all new model shall have this same property. And it’s relatively risk-less w.r.t.o inconsistencies as the specific case serves as a model in the sense of formal logic consistency.

However and again this is an axiomatic claim, not a fact: the world should be as we think it were, something that can not be proven, only disproven by a found counter-experiment. Similar as in the preceding cases of global claims, we will raise a red flag whenever Axiom 5.2 is actually used. (Question for the interested reader: why there can’t be a counter-experiment to axiom 5.3?)

With these considerations, we end the presentation of the first 5 Axiom-Sets for Q-Orders.

(1) Olaf Kummer and Mark-Oliver StehrPetri's Axioms of Concurrency - A Selection of Recent Results , Proceedings of the 18th International Conference on Application and Theory of Petri Nets, Toulouse, June 23-27, 1997, Lecture Notes in Computer Science 1248, © Springer-Verlag , 1997
(2) Mark-Oliver Stehr Cyclic Orders: A Foundation for Concurrent Synchronization Schemes. University Paris 7, Group Preuves, Programmes et Systemes, December 16, 2003. Part I: Thinking in Cycles

The Challenge

Albert Einstein

(1) Die allgemeinen Naturgesetze sind durch Gleichungen auszudrücken, die für alle Koordinatensysteme gelten, d.h. die beliebigen Substitutionen gegenüber kovariant (allgemein kovariant) sind.

Es ist klar, daß eine Physik, welche diesem Postulat genügt, dem allgemeinen Relativitätspostulat gerecht wird. Denn in allen Substitutionen sind jedenfalls auch diejenigen enthalten, welche allen Relativbewegungen der (dreidimensionalen) Koordinatensysteme entsprechen. Daß diese Forderung der allgemeinen Kovarianz, welche dem Raum und der Zeit den letzten Rest physikalischer Gegenständlichkeit nehmen, eine natürliche Forderungen ist, geht aus folgender Überlegung hervor. Alle unsere zeiträumlichen Konstatierungen laufen stets auf die Bestimmung zeiträumlicher Koinzidenzen hinaus. Bestände beispielsweise das Geschehen nur in der Bewegung materieller Punkte, so wäre letzten Endes nichts beobachtbar als die Begegnungen zweier oder mehrerer dieser Punkte. Auch die Ergebnisse unserer Messungen sind nichts anderes als die Konstatierung derartiger Bewegungen materieller Punkte unserer Maßstäbe mit anderen materiellen Punkten bzw. Koinzidenzen zwischen Uhrzeigern, Zitterblattpunkten und ins Auge gefassten, am gleichen Orte und zur gleichen Zeit stattfindenden Punktereignissen.

Die Einführung einen Bezugssystems dient zu nichts anderem als zur leichteren Beschreibung der Gesamtheit solcher Koinzidenzen. Man ordnet der Welt vier zeiträumliche Variable zu, derart, dass jedem Punktereignis ein Wertesystem der Variablen entspricht. Zwei koinzidierenden Punktereignissen entspricht dasselbe Wertesystem der Variablen ; d.h. die Koinzidenz ist durch die Übereinstimmung der Koordinaten charakterisiert. Führt man statt der Variablen beliebige Funktionen derselben, als neues Koordinatensystem ein, so dass die Wertesysteme einander eindeutig zugeordnet sind, so ist die Gleichheit aller vier Koordinaten auch im neuen System der Ausdruck für die raumzeitliche Koinzidenz zweiter Punktereignisse. Da sich alle unsere physikalischen Erfahrungen letzten Endes auf solche Koinzidenzen zurückführen lassen, ist zunächst kein Grund vorhanden, gewisse Koordinatensysteme vor anderen zu bevorzugen, d.h. wir gelangen zu der Forderung der allgemeinen Kovarianz.

The general laws of nature are to be expressed by equations, which are valid for all coordinate systems, ie. are covariant (generally covariant) in relation to the arbitrary substitutions.

It is clear that a physics, which meets this postulate, satisfies the general relativity postulate. Because in all substitutions anyhow are also those contained, which correspond to all relative motions (three-dimensional) of the coordinate systems. The fact that this demand of the general covariance, which takes away the last remainder of physical objectivity of space and time, is a natural demand, results from the following consideration. All our time-spatial stating always end in the determination of time-spatial coincidences. Would for example all events consist only in the motion of material points, then at least nothing would be observable but the meetings of two or several of these points. Also the results of our measurements are nothing else but stating such movements of material points on our yardsticks together with other material points respectively coincidences between watch-hands, points on clock-faces and observed point-events, taking place at the same time and at the same spot.

The introduction of a frame of reference serves for nothing else but for easier description of the totality of such coincidences. One assigns four time-spatial variables to the world such that the value-system of the variables corresponds to every point event. Two coinciding point events correspond to the same value-system of their variables; ie. the coincidence is characterized by the equality of the coordinates. If one uses instead of the variables any function of them as new coordinate-system, so that the values are unambiguously assigned to each other, the equality of all four coordinates also in the new system is the expression for the time-spatial coincidence of the two point events. Because all our physical experiences can be traced back after all to such coincidences, at first glance no reason exists to prefer certain coordinate systems over others, ie. we obtain the demand of general covariance.¹

(2) Man kann gute Argumente dafür anführen, dass die Realität überhaupt nicht durch ein kontinuierliches Feld dargestellt werden könne. Aus den Quanten-Phänomenen scheint nämlich mit Sicherheit hervor zugehen, dass ein endliches System von endlicher Energie durch eine endliche Zahl von Zahlen (Quanten-Zahlen) vollständig beschrieben werden kann. Dies scheint zu einer Kontinuums-Theorie nicht zu passen und muss zu einem Versuch führen, die Realität durch eine rein algebraische Theorie zu beschreiben.

Niemand sieht aber, wie die Basis einer solchen Theorie gewonnen werden könnte.

There are good reasons to suggest that nature cannot be represented at all by a continuous field. From quantum phenomena, it could be inferred with certainty that a finite system with finite energy should be described completely by a finite set of numbers (quantum numbers). This seems not in accordance with a continuum theory and obliges to attempt to describe reality by a purely algebraic theory.

But nobody has any idea of how to obtain the basis for such a theory.²

Carl Adam Petri established the ideas for a theory that may satisfy both Einstein postulates³.⁴

1 Albert Einstein, Die Grundlage der allgemeinen Relativitätstheorie, Annalen der Physik, 49 (1916), Pages 776,777

2 Albert Einstein, Grundzüge der Relativitätstheorie (1924), Reprint Springer Verlag, Page 163

3 Carl Adam Petri State-Transition Structures in Physics and in Computation. Int. Journal of Theoretical Physics, Vol. 21, No. 12, 1982, Pages: 979-992

4 Carl Adam Petri: On the Physical Basics of Information Flow. Petri Nets 2008: 12