The Great Simplification – Part II

After slashing the original definition of Axiom 6, here comes a similar reduction of Axiom 7, originally introduced in The trapped Arrow of Time – Part III.

The new
Axiom 7 Q-Loops
    
Axiom 7.1 are technical definitions:  completely Q-ordered sets and the closed hull of a set. 

Axiom 7.2-4 introduce a substitute for Jordan-Curves. 7.2 defines the property of being connect for a set in terms of topology. 7.3 defines the relation of being topologically separated for two points.  Please note that we don’t require that the whole space is T1. 7.4 defines J-Curves as sets that contain for each point at least one separated partner and fall apart exactly if a separated pair is removed. This definition requires implicitly the Axiom of Choice, therefore it’s flagged.

For the moment let’s assume that J-Curves exist -later on we will claim the existence of rather specific ones- and see whether the definition meets our expectations. Axiom 7.5 introduces the set of connected subsets into which a separated pair splits the J-Curve. By definition for J-Curves, there must be at least 2 of them.    
Lemma S 2 Segments  
 
The lemma shows that –as intended- a separated pair splits a J-Curve in just 2 segments. And these 2 segments contain at least each a point for a separated pair, that is we’ve got two pairs that mutually separate each other.

Sounds  familiar? Well, be aware that the term J-Curve was introduced and some of it’s properties shown without reference to the initial Q-Order, yet –as intended- on a J-Curve there exists a natural Q-Order, as defined by Axiom 7.6.
Lemma S 3 J-Order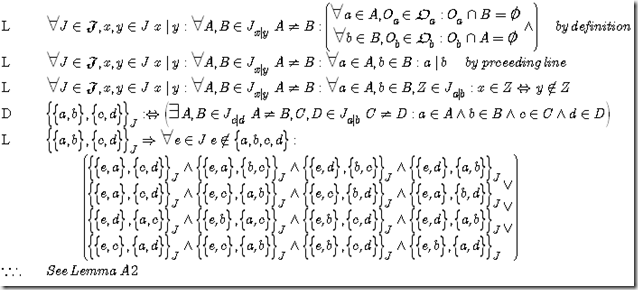 

Be aware that by no means all J-Curves correspond to q-ordered sets, as shown below.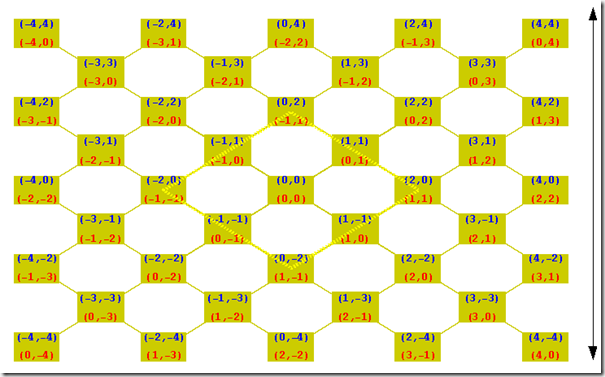 

The above yellow Rhombus  is a  J-Curve, yet it’s not a Q-ordered set but rather built by of 2 Q-ordered sets, the left and right side.

It appears as if we might start out just with some topology with some nice properties … and [re-]construct the Q-Order. For the moment we ask only –consistent with our whole approach- that every totally q-ordered set shall be consistently embeddable into some J-Curve, where consistency means that original Q-Order and derived Q-order of the curve are the same.

Axiom A 7.7 Consistent Embedding 

Axiom A 7.7 has backward consequences for the Q-topology.
Lemma S 4 Connected Space 
  
As immediate consequence of Axiom 7.6, J-Curves finally do exist. J-Curves connect the whole space (S 4.2), which is hence a connected topological space (S 4.3).

Finally
Axiom 7.8 Local Orientation

This Axiom establishes an intrinsic relation between J-Curves –remember they are closed- and the underlying Q-Topology. For each point –respectively its closed hull- there shall exist at least one neighborhood, sufficiently large that it can be split into two subsets –sometimes called local future and local past, or local input and local output- such that  each of these subsets is J-convex – i.e. any two points can be connected by a J-Curves, but sufficiently small that any J-Curve that connects between the sets contains at least one external point.

The picture below illustrates the concept.

The two sets are
{ {(0,0),(-1,0)}, (-1,0), {(-1,0),(-1,1)}, (-1,1), {(-1,1),(0,0)}, {(-1,1),(0,1)}, (0,1),{(0,1),(0,0)} }
{ {(0,0),(0,-1)}, (0,-1), {(0,-1),(1,-1)}, (1,-1), {(1,-1),(0,0)} {(1,-1),(1,0)}, (1,0),{(1,0),(0,0)} }

Axiom 7.8 requires at least two dimensions (or two J-Curves). As to be shown, it captures the  underlying  essence of the Hawking-construction  for regular curves, which in the original text is scattered between local properties of the manifold –existence of local convex neighborhoods in terms of the Manifold-Topology, global causality-conditions –strong causality-, all needed to effectively define Regular Curves, and finally the properties  defined by the construction as such.

This ends our preliminary presentation of the new Axiom 7 Q-Loops.