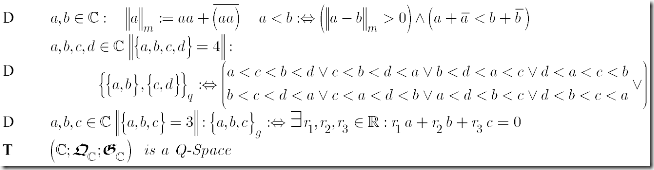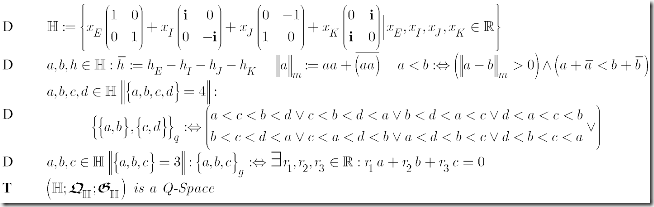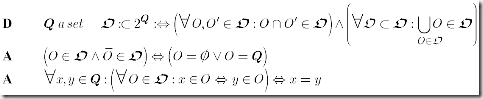The Axiom-Sets for Q-Spaces
There has been another round of silence in this BLOG, partially to attend some bread-and-butter business, partially to solidify the inclusion of a second basic relation besides order, a relation that reflects locally geometry: while the relation Q clearly models the conformal invariant structure –the Topology- of Space-Time, it misses the projective invariant part, which as shown by Hermann Weyl1 long time ago is needed to define the complete Einstein-Weyl Causality.
There as been a second change: while all earlier versions of the Axioms constructed the Topology using the Q-order relation, this version puts the definition of a class of Topologies at the beginning and then ties the Q-order relation to that topology. There are two reasons for this change: first it comes closer to the classical definition of the basic realm of classical General Relativity: a topological space with additional properties i.e. as differential manifold (which ties in geometric concepts) with an additional Lorentz-metric (which introduces order).
The second reason: the class of topologies singled out includes the topology of all Petri-Nets -without directions- and the topology of all locally path-connected spaces, which appears as the common topological ground for both: coarse graining a locally path-connected space such that grains are either open or closed one arrives at a Petri-Net and reverse: blowing up a Petri-Net i.e substituting its elements by convex open respectively closed sets one gets a locally path-connected space.
Introduction
We are searching for a combinatorial framework that, in an essential way, includes the structure of Space-Time as a continuous model on one side and the structure of of Petri-Nets as a finite (countable) model on the other.
Essential means that physically different Space-Times and logically different Petri-Nets shall have different models and that different models produce different Space-Times and different Petri-Nets respectively.
For Space-Times a seminal contribution of S. W. Hawking2 introduced a unique combinatorial structure –a partial-order– attached to Lorentzian Manifolds with some additional restrictions, that up to conformal mappings defines the manifold (review3 on Causal Space-times). David Malament4 showed how this combinatorial structure alone, under suitable conditions, is sufficient to reconstruct Space-time up to conformal factor.
There has been another approach somewhat close to ours. Hans-Jürgen Borchers and Rathindra Nath Sen reconstruct the complete Einstein-Weyl Causality5 starting from the total order on light rays. Light rays in a certain sense connect the conformal and the projective structure by their inherent order and being locally geodesic. Yet the authors still assume a global partial order and that light rays are order-dense, which precludes finite structures i.e. Petri-nets.
For Petri-Nets since 1973 there as been a systematic effort6 to detect the underlying combinatorial structures, specifically in the theory of Concurrency or causal structures defined by event-occurrence systems.
The problems
-
the mentioned Space-Time models in their definition make a heavy use of concepts typical for the continuous world, like Hausdorff-spaces as basic model-domain or using properties borrowed from Linear Algebra, all which as such can not be transported into the finite/countable domain.
-
the mentioned Petri-Net models -namely concurrency-theory- require countable models to work and therefore are as such a not suited to express all the technical concepts as used in continuous models. On structural level, there is no Linear Algebra, hence appears on first sight impossible to express concepts like convex let alone tensors or more complicated constructs.
-
Both models depend on Global Partial Orders even when expressing purely local concepts, a slight contradiction with the basic idea of General Relativity as something locally defined.
-
Geometry without additional constraints can not be derived from order alone. It must be introduced as an additional concept. It's long known that line-geometry -i.e. Geometry based on Points, Lines and Incidences- has finite, countable and continuous models. Yet the concept of a geodesic line is neither present in Causal Structures nor -as far as I know- in Petri Net-Theory.
The ideas for solution
-
Both model domains use Paths respectively Curves as a basic building block, where Curves in both domains model trajectories -world-lines- of particles (more precisely potential trajectories see7). All expressed relations and properties can be re-written using only curves and the relations among points as defined by curves.
-
As Petri pointed out quite early8, on partial orders there exists a generalization for the concept of Dedekind-continuity and -completeness that allows for countable models, yet if applied to full-orders produces the known results. Crucial are two types of points, closed and open, while retaining the idea that the emerging topologies should be connected.
-
A little bit later Petri proposed the separation relation {{a,b},{c,d}} -an unordered pair of unordered pairs- as the basic order-producing relation. This relation expresses the separation of 4 points on a line, and is well defined on any Jordan-Curve, open or closed, i.e. there is no difference between a line, may be with suitable compactification, and a circle.
-
A careful analysis of the original article from Hawking, specifically analyzing the relation between local time-like cones, which form the base for the topology, the definition of regular paths in that topology and their relation to time-like curves, allowed to eliminate the reference to linear concepts like convex and to define local time-like cones and their properties using only combinatorial concepts.
-
This revision in turn demanded a revision of concepts in Petri-Nets. While in the original model the open elements are conditions and the closed elements are the events, and likewise sets border by conditions considered open while sets bordered by events closed, we need exactly the dual: events and event-bordered sets are open, conditions and condition-bordered sets are closed. It should be noted that for countable structures -Petri-nets are normally assumed to be countable- both sets -open and closed- define the same dual Alexandrov9Topology. However already the comparison of Dedekind continuity between total orders and half-orders alas Occurrence-Nets shows that the common type of elements in both -the non-branching conditions- must be closed.
-
In a Hawking-space all points are closed. Therefore it was necessary to overcome the initial interpretation of Einstein as if world points would correspond to physical events. They do not! If a Hawking-space models the loci -the geometry-, then a physical event can not have an exact place as Quantum-Mechanics tells us. A similar observation made decades ago Pauli10. Curiously enough, in this interpretation nothing ever happens in Hawking-Space as there are no events. To have events we must coarse grain first.
-
Likewise a too naive interpretation by Net-Theory of GRT had to be abandoned, as if each world-point branches into infinite many world-lines. Actually a world-point summarizes the whole time-like pre- respectively post-cones as such and not individual lines. This is the essence of the construction of regular paths by Hawking and the distinguishing conditions from Malament.
-
W.r.t. Geometry, we will start at the most elementary level: locally a line shall be uniquely defined by 2 points, locally any 2 points shall be connected by a line, finally the geometry shall be non-trivial i.e the local space shall be connected by lines with at least 3 points. Obviously, once defined, lines shall split into the three known classes: time-like, light-rays, space-like.
1 Hermann Weil, Zeit-Raum-Materie, III. Edition, Julius Springer Verlag, Berlin, 1919
2 S. W. Hawking A.R. King and P. J. McCarthy,
A new topology for curved space-time which incorporates the causal, differential and conformal structures Journal of Mathematical Physics Vol. 17, No 2, February 1976
3 Alfonso García-Parrado, José M. M. Senovilla,
Causal structures and causal boundaries,
arXiv:gr-qc/0501069v2 4 D. Malament,
The class of continuous timelike curves determines the topology of spacetime Journal of Mathematical Physics, July 1977, Volume 18, Issue 7, pp. 1399-1404
5 Hans-Jürgen Borchers, Rathindra Nath Sen, Mathematical Implications of Einstein-Weyl Causality, Lect. Notes Phys. 709 (Springer, Berlin Heidelberg 2006)
6 Olaf Kummer, Mark-Oliver Stehr:
Petri's Axioms of Concurrency - A Selection of Recent Results , Proceedings of the 18th International Conference on Application and Theory of Petri Nets, Toulouse, June 23-27, 1997, Lecture Notes in Computer Science 1248,
© Springer-Verlag , 1997
7 David B. Malament,
Classical Relativity Theory,
arxiv.org/abs/gr-qc/0506065v2 8 Petri, C.A.,
Concurrency. Lecture Notes in Computer Science Vol. 84: Net Theory and Applications, Proc. of the Advanced Course on General Net Theory of Processes and Systems, Hamburg, 1979 / Brauer, W. (ed.) --- Berlin, Heidelberg, New York: Springer-Verlag, 1980, Pages: 251-260
9 Not to be confused with the Alexandrov Topology used by Hawking
10 Pauli,
Vorlesungen in Turin über nichtlokale Feldtheorien in Google-Books
http://books.google.com/books?id=NU9OUj-f8cYC&hl=es Page 34 ff.
Based on the above I obtained the Axiom-sets shown below. In the second part of this post we will comment on each set.
The Axioms
The Topology and Q-Order Axioms 
Geometry and Compatibility Axioms 
The Axiom-sets group by group
Topology Axioms
Axiom 1 TOP Topological Space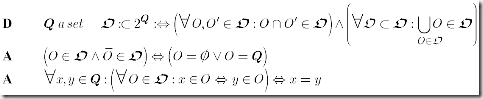
Axiom TOP defines a Topology with 2 additional properties, connected and distinguishing or T0 i.e. different points have different open neighborhoods.
Axiom 2 PAT Path connected

Normally locally path-connected is defined by the existence of a continuous mapping of the [0,1] interval into the space or subs-spaces. As this mapping carries some of the topological characteristics of R, we first define one-dimensional connected subspaces J, and then claim the existence of neighborhoods where all points are connected by some of these subspace in J (the letter reflects Jordan-Curves, actually sub-spaces in in J are the traces of continuous, monotone mappings of S1)
Local Q-Order Axioms
Axiom 3 REL Q-Relation 
Axiom 4 LIN Q-Linear 
Axiom 5 ORD Q-Ordered

The above Q-Order Axioms remain unchanged compared to earlier versions. The model the situation of points on closed curves. For details and the underlying heuristics please consult: Revised: Going in Circles – Part I and Revised: Going in Circles – Part II.
Global Orientation of Q-Orders
Axiom 6 ORI Q-Oriented

Axiom ORI combines into a single Axiom-set the necessary and sufficient conditions to extend an orientation once it’s define on a single circle. For details and the underlying heuristics please consult: Revised: Going in Circles – Part III. It should be noted that partial orders without identical points satisfy all the above Q-Order Axioms. The formal proof that a Lorentzian Causal Order is orientable iff it’s orientable in the sense of Q-orders is still incomplete.
Generalized Dedekind Completeness of Q-Orders
Axiom 7 COM Q-Complete
 Axiom COM is a localized version of the Generalized Dedekind Completeness for partial orders as introduced first by Carl Adam Petri. Whereas the original version by Petri and our own introduces and uses Lines as maximal totally ordered sets, this version uses only totally ordered Intervals. The essence that any d-cut that cuts an interval defines a unique limit point for that interval, remains the same. Crucial is the distinction between border points bdr and limit points lim. is For details and the underlying heuristics please consult: Lines, Cuts and Dedekind.
Axiom COM is a localized version of the Generalized Dedekind Completeness for partial orders as introduced first by Carl Adam Petri. Whereas the original version by Petri and our own introduces and uses Lines as maximal totally ordered sets, this version uses only totally ordered Intervals. The essence that any d-cut that cuts an interval defines a unique limit point for that interval, remains the same. Crucial is the distinction between border points bdr and limit points lim. is For details and the underlying heuristics please consult: Lines, Cuts and Dedekind.
When thinking in Lorentzian Causal Order, remember that Q-Orders correspond to time-like curves, hence the tip of a time-like cone (i.e. a light-cone without its border) is a limit to the whole cone, not only to each of its lines. If –as in non-distinguishing causal structures see David Malament4 - there are more but one tip-point, these are not time-like to each other, hence they remain unique for each time-like curve. In the case of Q-Orders and Petri-Nets, limit points are the single-entry – single exit elements. A Q-complete Petri-Net resembles an occurrence-net with conditions as limits.
Compatibility between Q-Order and Topology
Axiom 8 CON Q-Continuous

Axiom CON claims the compatibility between limit-points and closed points in the underlying topology, and sets which contain an interval for each of its closed points and open sets of the underlying topology. In Q-Topology – I we showed that the Q-order Axioms themselves are sufficient to construct a topology. In a yet to be published post we will show that this topology satisfies the new Topology Axioms. Moreover topology + incomplete Q-Order for the countable case still define a globally orientable Petri-Net. Finally there is a procedure to complete Q-orders, such that the completed Q-Order is compatible.
Geometry Axioms
Axiom 9 GEO Geometry
 The Geometry-Axioms try to capture the most elementary of a local geometry. The second line defines a new three-element unordered relation g. The third line defines normal sets as sets which (1) are connected by the geometry-relation, where (2) different elements can be separated and (3) any three points define a unique set of g-related elements. Before looking into more details, let’s translate these conditions in the usual terminology for Incidence Geometry.
The Geometry-Axioms try to capture the most elementary of a local geometry. The second line defines a new three-element unordered relation g. The third line defines normal sets as sets which (1) are connected by the geometry-relation, where (2) different elements can be separated and (3) any three points define a unique set of g-related elements. Before looking into more details, let’s translate these conditions in the usual terminology for Incidence Geometry.
Definition 1 Linear Space

The first line defines the set of lines belonging to a normal set. The following Lemmata are straight forward almost by definition: (1) any two points lie on at least 1 line, any line has at least 2 different points on it. (2) any point lies on at least 2 different lines and finally (3) 2 different lines cut each other at at most 1 point. The later implies that 2 points define a unique line.
These structures are well known as Linear Spaces. The structure arises naturally if ones selects or finds a set a set of points out of a projective or affine geometry or similar, with the additional constraint that the set shall be distinguishing: different points differ in at least one line they lie on. Or from a different perspective: it’s what one obtains by selecting points out of a normal neighborhood of a Lorentzian Manifold, taking the geodesics as lines.
Going back to Axiom GEO any point shall be contained in some normal set and the class of normal sets connected w.r.t. to g.
Compatibility between Q-Order and Geometry
Axiom 10 COH Q-Coherent
 The axiom claims that light-rays are geodesic and that any geodesic is either time-like, space-like or light-like. The explanation and heuristics for the crucial second definition of light-ray related will be provided soon.
The axiom claims that light-rays are geodesic and that any geodesic is either time-like, space-like or light-like. The explanation and heuristics for the crucial second definition of light-ray related will be provided soon.
Problems remaining
We would like to embed Linear Structures into Vector-spaces as an initial step towards the construction of Tangent-bundles, which will be needed if we would like to have something like Field-equations