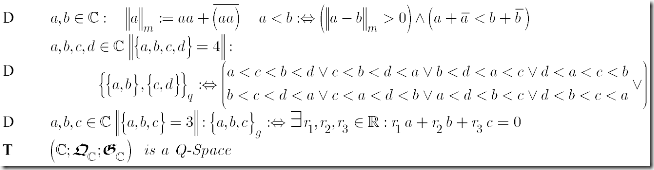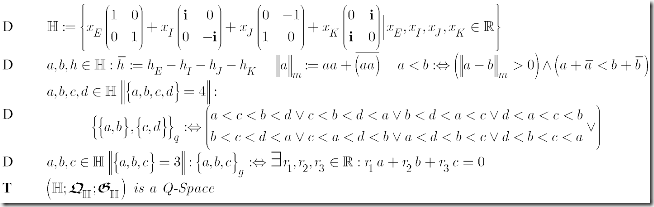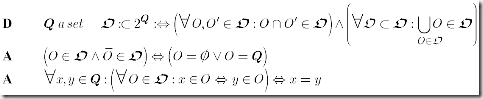Introduction
We are looking for a combinatorial framework that, in an essential way, includes the structure of Space-Time as a continuous model on one side and the structure of of Petri-Nets as a finite (countable) model on the other.
Essential means that physically different Space-Times and logically different Petri-Nets shall have different models and that different models produce different Space-Times and different Petri-Nets respectively.
A wrong way to get time & space would be simply to assume them, as Einstein showed convincingly more but a century ago, refuting thereby Immanuel Kant, who another century before had declared time & space as logical “a priori” beyond material experience.
{Here and later on we will use deliberately time-space instead of the usual space-time when referring to our model}.
There is a second caveat already raised by Einstein –see The Challenge-:
At the very end, all measurement (and hence all Physics) boils down to have/to observe the coincidence of something at the same time-space point, while the description of time-space points using coordinates is just a convenient means to describe these coincidences. Hence it should make no difference in the description at least, if another such system of coordinates is used, if only there is a one-to-one correspondence between the former and the latter.
Though a specific time & space may be extremely practical for a description and hence a necessary heuristic tool -among other to detect symmetries which reflect physical invariants-, the Physics described should not depend on the specifics of the used space & time: Any time & space should do, as long it produces the same pattern of coincidence.
The principle of General Covariance, even more its expression as diffeomorphism covariance, is for Einstein a sequitur of the idea of background independence. Actually he uses –and others since- nonetheless only these very specific coordinate-systems, that are appropriate for the description of Differential Manifolds. Yet he never stated anywhere that the realm of Differential Manifolds would be for him the only domain for admissible Coordinate-Systems.
Without getting here into more of the heuristic details, why it might be convenient to use less sophisticated structures for the sake of the spirit of GRT itself, in this article we will introduce an axiom-set of 5 groups of axioms, which uses just very elementary concepts from set-topology without any metric, yet by the end provides a Category of Topological Spaces powerful enough to include in a non-trivial way Differential Manifolds with Lorentzian metric but also other finite and countable models. Finite and countable models turn out to be Petri-Nets with additional interpretation.
{Non-trivial means that any diffeomorphism of the manifold implies a corresponding homeomorphism in this category, including the required updates of time & geometry.}
Related approaches
For Space-Times a seminal contribution of S. W. Hawking[1] introduced a unique combinatorial structure –a partial-order– attached to Lorentzian Manifolds with some additional restrictions, that up to conformal mappings defines the manifold (Alfonso García-Parrado and José M. M. Senovilla review[2] on Causal Space-times). David Malament[3] showed how this combinatorial structure alone, under suitable conditions, is sufficient to reconstruct Space-time up to a conformal factor.
Rafael Sorkin[4] and his school used the above results to establish the concept of a Causal set, an interval-finite, combinatorial model. Yet there is no direct structural link to the originating structure and they try to complete in one step the model presenting volume as the only missing concept, similar as John Stachel[5] proposes on a continuous background to combine projective and conformal structure. We decided to do one step at a time that is first combine both concepts before jumping into metrics. And –quite different to the Causal Set approach- we insist that there must be a structural connection between the discrete and the continuous model.
There has been another approach somewhat close to ours. Hans-Jürgen Borchers and Rathindra Nath Sen reconstruct the complete Einstein-Weyl Causality[6] starting from the total order on light rays. Light rays in a certain sense connect the conformal and the projective structure by their inherent order and being locally geodesic. Yet the authors still assume a global partial order and that light rays are order-dense, which precludes finite structures i.e. Petri-nets.
For Petri-Nets since 1973 there as been some systematic effort; Olaf Kummer and Mark-Oliver Stehr present some more recent results[7] to detect the underlying combinatorial structures, specifically in the theory of Concurrency or causal structures defined by event-occurrence systems.
The problems
- the mentioned Space-Time models in their definition make a heavy use of concepts typical for the continuous world, like Hausdorff-spaces as basic model-domain or using properties borrowed from Linear Algebra, all which as such can not be transported into the finite/countable domain.
- the mentioned Petri-Net models -namely concurrency-theory- require countable models to work and therefore are as such a not suited to express all the technical concepts as used in continuous models. On structural level, there is no Linear Algebra, hence appears on first sight impossible to express concepts like convex let alone tensors or more complicated constructs.
- Both models depend on Global Partial Orders even when expressing purely local concepts, a slight contradiction with the basic idea of General Relativity as something locally defined.
- Geometry without additional constraints can not be derived from order alone. It must be introduced as an additional concept. It's long known that line-geometry -i.e. Geometry based on Points, Lines and Incidences- has finite, countable and continuous models. Yet the concept of a geodesic line is neither present in Causal Structures nor -as far as I know- in Petri Net-Theory.
The ideas for solution
- Both model domains use Paths respectively Curves as a basic building block, where Curves in both domains model trajectories -world-lines- of particles (more precisely potential trajectories see Malament[8]). All expressed relations and properties can be re-written using only curves and the relations among points as defined by curves.
- As Carl Adam Petri[9] pointed out quite early, on partial orders there exists a generalization for the concept of Dedekind-continuity and -completeness that allows for countable models, yet if applied to full-orders produces the known results. Crucial are two types of points, closed and open, while retaining the idea that the emerging topologies should be connected.
- A little bit later Petri proposed the separation relation {{a,b},{c,d}} -an unordered pair of unordered pairs- as the basic order-producing relation. This relation expresses the separation of 4 points on a line, and is well defined on any Jordan-Curve, open or closed, i.e. there is no difference between a line, may be with suitable compactification, and a circle.
- A careful analysis of the original article from Hawking, specifically analyzing the relation between local time-like cones, which form the base for the topology, the definition of regular paths in that topology and their relation to time-like curves, allowed to eliminate the reference to linear concepts like convex and to define local time-like cones and their properties using only combinatorial concepts.
- This revision in turn demanded a revision of concepts in Petri-Nets. While in the original model the open elements are conditions and the closed elements are the events, and likewise sets border by conditions considered open while sets bordered by events closed, we need exactly the dual: events and event-bordered sets are open, conditions and condition-bordered sets are closed. It should be noted that for countable structures -Petri-nets are normally assumed to be countable- both sets -open and closed- define the same dual Alexandrov[10] Topology. However already the comparison of Dedekind continuity between total orders and half-orders alas Occurrence-Nets shows that the common type of elements in both -the non-branching conditions- must be closed.
- In a Hawking-space all points are closed. Therefore it was necessary to overcome the initial interpretation of Einstein as if world points would correspond to physical events. They do not! If a Hawking-space models the loci -the geometry-, then a physical event can not have an exact place as Quantum-Mechanics tells us. A similar observation made decades ago Pauli[11]. Curiously enough, in this interpretation nothing ever happens in Hawking-Space as there are no events. To have events we must coarse grain first.
- Likewise a too naive interpretation by Net-Theory of GRT had to be abandoned, as if each world-point branches into infinite many world-lines. Actually a world-point summarizes the whole time-like pre- respectively post-cones as such and not individual lines. This is the essence of the construction of regular paths by Hawking and the distinguishing conditions from Malament.
- W.r.t. Geometry, we will start at the most elementary level: locally a line shall be uniquely defined by 2 points, locally any 2 points shall be connected by a line, finally the geometry shall be non-trivial i.e the local space shall be connected by lines with at least 3 points.
[1] S. W. Hawking A.R. King and P. J. McCarthy, A new topology for curved space-time which incorporates the causal, differential and conformal structures Journal of Mathematical Physics Vol. 17, No 2, February 1976
[2] Alfonso García-Parrado, José M. M. Senovilla, Causal structures and causal boundaries, arXiv:gr-qc/0501069v2
[3] David Malament, The class of continuous timelike curves determines the topology of spacetime Journal of Mathematical Physics, July 1977, Volume 18, Issue 7, pp. 1399-1404
[4] Rafael Sorkin, Causal Sets: Discrete Gravity, Notes for the Valdivia Summer School, Jan. 2002, arXiv:gr-qc/0309009v1 1 Sep 2003
[5] John Stachel, Projective and Conformal Structures in General Relativity, Loops ’07, Morelia June 25-30, 2007,
[6] Hans-Jürgen Borchers, Rathindra Nath Sen, Mathematical Implications of Einstein-Weyl Causality, Lect. Notes Phys. 709 (Springer, Berlin Heidelberg 2006)
[7] Olaf Kummer, Mark-Oliver Stehr: Petri's Axioms of Concurrency - A Selection of Recent Results , Proceedings of the 18th International Conference on Application and Theory of Petri Nets, Toulouse, June 23-27, 1997, Lecture Notes in Computer Science 1248, © Springer-Verlag , 1997
[8] David B. Malament, Classical Relativity Theory, arxiv.org/abs/gr-qc/0506065v2
[9] Carl Adam Petri, Concurrency. Lecture Notes in Computer Science Vol. 84: Net Theory and Applications, Proc. of the Advanced Course on General Net Theory of Processes and Systems, Hamburg, 1979 / Brauer, W. (ed.) --- Berlin, Heidelberg, New York: Springer-Verlag, 1980, Pages: 251-260
[10] Not to be confused with the Alexandrov Topology as used by Hawking
[11] Pauli, Vorlesungen in Turin über nichtlokale Feldtheorien in Google-Books http://books.google.com/books?id=NU9OUj-f8cYC&hl=es Page 34 ff.
The Axioms for Einstein-Spaces
Based on the above I obtained Axioms for Einstein-Spaces as presented below.
Some models for E-Spaces are:
(1) Occurrence-Nets (with the above change and some additional requirements) as subclass of Petri-Nets
(2) The Real Numbers (but not Rationales nor Integers) (Q-order is derived from classical order)
(3) The Unit-Circle S1 (and the Circle Group) (but not n-cyclic Groups) and the Real Line (Q-order is derived from the relation among four points)
(4) The Minkowski-Space and the Quaternion (Q-order is derived from Q-Topology)
(5) The Causal structure of a Lorentzian manifold as defined by Hawking and others (Q-order is derived from the relation among four points on a time-like curve)
{For more see E-Space Examples, though it’s not yet updated to the most recent findings of this version for the axioms.}
Axiom 1 A–Space Atomic Topological Space
Axiom-set 1 presents an almost standard definition for a Topology (1,6) and its homeomorphisms (2).
(2) will serve us as test-instrument: what not remains invariant will not be acceptable.
(3) introduces the notion of closure and interior operation. (4) is a may be not-so-usual but equivalent way to define connected for a set.
(5) singles out the subsets of closed respectively open elements. Be aware that we do not ask all elements to be closed, just either closed or open (9). The name atomic is our invention. As shorthand we will call point only the closed elements and add open where required.
(7) defines the topology as connected, (8) eliminates topologically equivalent elements and finally (10) requires the existence of a countable dense subset, the usual definition for separable.
{Only natural numbers were made by God Himself, anything else is human invention, as Kronecker always said.}
{As well known results from set-topology, the properties (7), (8), (9) (10) are topological invariants}
{By definition a manifold complies with Axiom 1}
As here, in the sequel we will use the letter D to introduce a definition-line, A for a line that claims a property as axiom. As a hint: you may open a larger picture of each axiom in a second window just by clicking .. and then switch between image-window and text … to avoid loosing the reference context.
Before starting the presentation of Axiom 2, some heuristics about what we would like to achieve.
- We are looking for a substitute for the usual definition of geodesics yet without using any metric concept, where any shall be understood literally that is we refuse even to rely on an underlying Euclidean metric space as the usual definition of a manifold does. Hence we can not use concepts from differential calculus either, as they do require at least a normed linear vector-space. Yet in combinatorial geometry –where we may perfectly define affine, projective or simpler linear spaces- there is also no differential calculus necessary.
- The most simple combinatorial structure is the Linear Space with Lines and Points such that any two points are on at least one line, each line has at least two points, two different lines share at most one point and finally two different points are on at least two different lines. This structure can be extended by a canonical procedure into a projective plane, preserving the initial lines. This purely combinatorial structure seems as a good candidate, moreover as –if desired- we may add additional properties to require right from the outset a projective or affine geometry without touching metrics.
- The definition of geodesics in GRT is strictly local i.e. applies only in local context. We will need some means to define this context, yet assure consistency of the definitions, similar as it’s done in sheaf-theory.
- The definition has to be background-independent or -what is the same in our limited world of Topology- a topological invariant w.r.t. homeomorphisms.
- The final idea had parents: Albert Einstein, with his famous equivalence principle –there is no difference if someone moves on a geodesic or stays put yet the world moves around him- and Ruth Moufang, who introduced Lines as fix-points for translation-symmetries in combinatorial geometry. As a child idea, we will try to define a geodesic as the local fix-point for those global homeomorphisms (obviously a subgroup) that move us along the geodesic. If successful, we are done, as homeomorphisms map subgroups.
Axiom 2 G–Space Geometric Space 
Axiom-set 2 adds a property to A-Space (1).
Blocks (2) –our local context to be used- are closed subspaces, for which all open neighborhoods contain another open neighborhood within which they are connected (Beware: as we may have open elements, the intersection of all open neighborhoods of a point/a closed set may contain still other elements besides the point/the set itself).
For the same reason (4) we consider initially only points as elements of Pre-Geodesics, applying some technicalities (5) later to add may be missing elements.
{Yet –without getting into details now, but important for the later work- this allows some at the first sight strange geometries with strange geodesics (geodesics of points all with a rational ratio of their intervals on the Real line.). If all elements are closed, then (5) is void, i.e. nothing is added.}
(3) Is the cornerstone of the axiom-set: It defines a predicate γ that combines blocks and subsets of points, and delivers true when they match the conditions.
- (3.1) is more technical: any local subset of a pre-geodesic is a pre-geodesic.
- (3.2) and (3.3) express partially the requirements for Linear Spaces: any point is on some pre-geodesic with at least 2 points. If two pre-geodesic share more than 2 points, they are part of another pre-geodesic. Take a chain of these, then the maximal element is the one and only one on which all the points are.
- (3.4) Tries to implement the child-idea: for any 2 local points on a pre-geodesic, there exists a global homeomorphism that carries one onto the other (the world moves, 3.4 first half), yet this homeomorphism carries also the whole pre-geodesic in a way that the original point joined to the local part of the image form again a pre-geodesic (3.4 second half). It shares with the original pre-geodesic 2 points. Hence their join is part of the same maximal pre-geodesic (3.3).
- The moving homeomorphisms form a subgroup of the homeomorphism-group of the A-topology, which leaves invariant the maximal element (the one and only one, voilá our fix-point). This subgroup is an invariant of the homeomorphism-group itself, that is when mapping the points, the sub-group is mapped accordingly. Hence as final result (3.1), (3.2)and (3.3) remain likewise intact.
(4) Constructs the class of all possible pre-geometries, admitting only those whose permitted blocks form a cover for the set of points.
(5) Adds elements in case that not all elements of the set are points. (Beware: we do not ask that a pre-geodesic to be topologically connected. Neither pre-geodesics nor geodesics are necessarily topological paths i.e. images of a continuous mapping of [0,1]. They rather will serve to measure (or count) not to define topology.
{As a hint: a physical light-ray considered as geodesic can not be connected topologically, due to the quantum-nature of light. Yet it follows a topologically connected path with distance measure 0, at least as long as we don’t get into QED.}
(6) Contains another part of the Linear Space requirements: once completed, (6.1) connects a block using now geodesics and (6.2) assures that all elements can be told apart using geodesics. I named this set of requirements G-Definite .
(7) Appears as if it were a repeat of (4), now for geometries. Well, it’s not!
The class contains geometries as completed in (5), yet the predicate γ is only applied to the original pre-geometry, while definiteness is tested for the completed geometry.
{Beware: a completed geodesic may contain open elements, which would cripple γ right away: you can not move an open onto a closed element and vice-versa. Likewise we do not require that the topology is homogeneous in all points. As will be needed later elsewhere, some points will correspond to observables, others are unobservable details. All obviously only in the case that the topology has open elements.}
(8) Is finally the axiom itself. The class of geometries is not empty i.e. there is at least one. And if there is one … there are many as we can move around using the homeomorphism-group. That’s the content of the Theorem (9).
{The crafting or la carpintería wasn’t done yet. However all the definitions above are based only on the A-topology or (3) firmly tied to it. So it should/might be tedious but appears true and feasible to compose if minor details are still wrong.}
{Now take a Lorentzian Manifold, use as one initial geometry the geodesics of the corresponding Lorentzian metric, take as blocks the closure of some normal neighborhoods for each point, such that their join forms a cover. Then it appears as if this geometry satisfies at least (3.1), (3.2), (3.3), (6.1), (6.2).
The missing part: find the move-around diffeomorphism. Well, I’m not very rapid/clever/trained in Lorentzian Manifolds, but again it appears to me that they do exist. It might take some time –more time for me- but appears to me as a feasible approach.
Done this, (5) is void as the underlying Topology is Hausdorff, hence there is no difference between (4) and (7). Finally a even larger class results from applying the diffeomorphism to the initial geometry according to (9).}
We will leave G-Spaces and turn our attention to another way to add properties, based on curves, to an A-Topology. Basically these combinatorial structures –some times called Space-Time, sometimes Causal Structure are fairly well known since David Malament proved his famous equivalence-theorem about time-like curves and causal structure of a Lorentzian Manifold.
Yet all these approaches –or at least many of them- introduce a very basic asymmetry between Time and Space: while the former is assumed to be some type of partial order with hence no closed time-like (causal) curves, the authors do not put the same type of restriction on Space, where a closed (spatially) universe is still an option.
In other entries of my BLOG I explain why I don’t share this approach, which more over heavily relies on arguments outside GRT itself (like the famous Grandfather paradox) and –in my humble opinion- enters into open contradiction with very basic assumptions of GRT. We need something to replace Partial Order as a building block while retaining orientability. This is the central attempt of Axiom 3 and Axiom 4.
Axiom-set 3 starts (1) with some A-Space.
(2) defines as pre-path sets that fall apart if –except may be end-elements Z- a single element is removed. It’s an attempted replacement for the classical definition of [the image] of a Jordan-curve, yet without using the whole baggage of Real-Topology and intrinsically substituting the concept of injective by monotone, needed as the A-Topology is not required to be Hausdorff.
(3) extends the idea to closed curves. Both together form paths. Please note we are talking about images, so there is no parameter nor parameterization, which again would introduce metric concepts at a far to early stage.
(4) defines which sets we will consider path-connected, such that (5) may claim that for every element every open neighborhood contains a path-connected open neighborhood. Elements neither closed nor open would damage these definitions. Finally path-connected extends to the whole set, as it’s itself connected (A 1.7) {well known result from set-topology}.
(6) Eliminates loose ends i.e. any element has at least two neighbors.
{As well known result from set-topology, paths themselves and the above definitions based on paths are topological invariants}
{As well known result any manifold complies with Axiom 3}
Paths define a symmetry-relation among their elements: the order by which they are arranged on the path. This relation is known since ancient times. The next theorem explores this relation.
Theorem 1 Q–Relation 4 elements on a path
(1) sets the domain: we will talk about the paths of a P-Space.
(2) defines the Q-Relation: 4 elements may be grouped into two pairs such that each pair separates the other (5).
(3), (4), (5) explore the relation (details in the referred entries).
(6) shows that the Q-Relation is persistent i.e. once defined it does not change in broader settings, a property important later on for instance for approximations.
(7) shows that the Q-Relation is a topological invariant, almost obvious by looking at (2) and recalling that paths themselves are invariant.
The next step consists in introducing a combinatorial concept for time. To put it very bluntly, we will do as mankind already has done: simply extended/extrapolate to the whole universe, what we know already for sure from one path -by the way, due to Theorem 1, any path-, that is we assume that there is a structure that behaves almost like a path. This structure we call a time.
(1) sets the domain: we will talk about the paths of a P-Space.
(2) introduces the structure time we are looking for, in which the Q-Relation shall hold if it holds for any member-path.
(3) is just a simplification of the Q-Relation: We forget the order and only remember that the 4 elements are on some path.
(4) defines a predicate θ, true if the structure behaves like we assume it does (i.e. like a path). (The entry Going around in Circles I explores its meaning).
(5) Defines a rule of interference to combine different paths of a time.
(5.1) whenever all pairs of 3 points can be found on some path –regardless their configurations there-, there should be a 4th element to give a complete path, where all 4 may be positioned.
(5.2) whenever all triplets of 4 points are on some path, the 4 points themselves may be positioned on a path.. (The entry Going around in Circles II provides some heuristics for this rule and shows its consequences).
(6) states the already familiar concept we used for topology and geometries that elements are connected yet may be separated using only time.
Done? Well not yet. A path is a topologically connected structure. Therefore the interval between two points is always open. The predicate (7) carries this on to time.
{In GRT time-like cones and time-like double-cones are always open.}
(8) Defines the class of possible time(s) while (9) as axiom claims that this class is not empty.
(10) shows that time(s) are a topological invariants, almost obvious as we used only paths, the Q-Relation and the topology itself to define time(s).
In the next step, we will combine time(s) and geometries into a single framework.
Axiom 5 E–Space Spaces with Time and Geometry
(1) sets the domain: we will talk about spaces that have both time and geometry.
There is a compatibility condition, well known from GRT: a geodesic once time-like remains time-like. This condition is expressed by (2).
(3) as axiom claims that there is at least one compatible pair of (time,geometry).
{The compatibility condition rules out effects at distance, spooky effects as Einstein calls them in the Einstein-Rosen paradox. Yet it does not exclude symmetries at distance of the geometry, that’s Bell or not Bell is not a question, at least in our Einstein Spaces.}
{Take as a Time the time-like curves of a Lorentzian Manifold, as Geometry the geodesics of a cover by normal neighborhoods, then the manifold becomes an Einstein-Space. }
Our principal theorem:
Theorem 2 Einstein Spaces E – Spaces form a Topological Category
(1) defines just the class of homeomorphisms between two topological spaces.
(2) states that if they are isomorphic w.r.t to their topology, then one of them is an E-Space iff the other is also an E-Space, that is E-Spaces form a Category of topological spaces, which we call Einstein-Spaces.
{The crafting or la carpintería wasn’t done yet. However from earlier remarks, it seems quite obvious that G-Spaces and T-Spaces each are topological categories. The compatibility condition as such is topologically invariant.}
We add two pages with the bare-bone axiom-sets and theorems. 
{If Theorem 2 is true, then it might have far reaching consequences.
At least to me it would explain a lot about the intrinsic, tricky relation between the Einstein Field-Equation –it appears as if it combines Geometry and Physics- on one side and Causal Structure -in the sense of Hawking and Malament- on the other, which may be modeled quite naturally as a Time. The solution to this puzzle would come close to solve the second Einstein Challenge, still an arduous task for many researchers and thinkers far better equipped with mathematical and physical background than I am, but unsolved now for almost a 100 years).}
We’re done!
Cornelius Hopmann, December 2010